¶ 1995 AIME Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 1995 AIME problems here.
Discussion Forum
Engage in discussion about the 1995 AIME math contest by visiting Random Math AIME 1995 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 1995 AIME problems, please refer below:
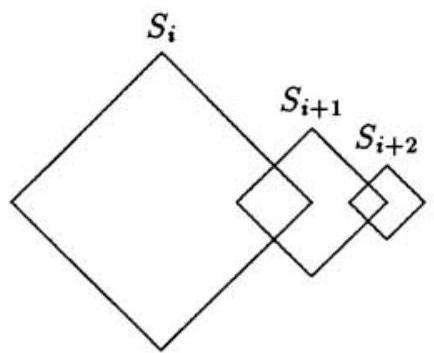
Problem 1: Square is . For , the lengths of the sides of square are half the lengths of the sides of square , two adjacent sides of square are perpendicular bisectors of two adjacent sides of square , and the other two sides of square are the perpendicular bisectors of two adjacent sides of square . The total area enclosed by at least one of can be written in the form , where and are relatively prime positive integers. Find .
Solution:
Problem 2: Find the last three digits of the product of the positive roots of
Solution:
Problem 3: Starting at , an object moves in the coordinate plane via a sequence of steps, each of length one. Each step is left, right, up, or down, all four equally likely. Let be the probability that the object reaches in six or fewer steps. Given that can be written in the form , where and are relatively prime positive integers, find .
Solution:
Problem 4: Circles of radius and are externally tangent to each other and are internally tangent to a circle of radius . The circle of radius has a chord that is a common external tangent of the other two circles. Find the square of the length of this chord.
.jpg)
Solution:
Problem 5: For certain real values of , and , the equation has four non-real roots. The product of two of these roots is and the sum of the other two roots is , where . Find .
Solution:
Problem 6: Let . How many positive integer divisors of are less than but do not divide ?
Solution:
Problem 7: Given that and
where , and are positive integers with and relatively prime, find .
Solution:
Problem 8: For how many ordered pairs of positive integers , with , are both and integers?
Solution:
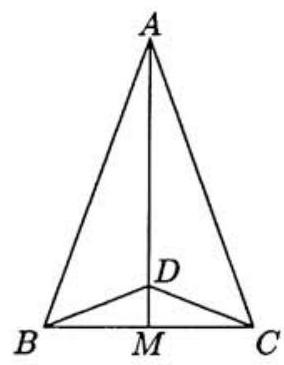
Problem 9: Triangle is isosceles, with and altitude . Suppose that there is a point on with and . Then the perimeter of may be written in the form , where and are integers. Find .
Solution:
Problem 10: What is the largest positive integer that is not the sum of a positive integral multiple of and a positive composite integer?
Solution:
Problem 11: A right rectangular prism (i.e., a rectangular parallelepiped) has sides of integral length , with . A plane parallel to one of the faces of cuts into two prisms, one of which is similar to , and both of which have nonzero volume. Given that , for how many ordered triples does such a plane exist?
Solution:
Problem 12: Pyramid has square base , congruent edges , and , and . Let be the measure of the dihedral angle formed by faces and . Given that , where and are integers, find .
Solution:
Problem 13: Let be the integer closest to . Find .
Solution:
Problem 14: In a circle of radius , two chords of length intersect at a point whose distance from the center is . The two chords divide the interior of the circle into four regions. Two of these regions are bordered by segments of unequal lengths, and the area of either of them can be expressed uniquely in the form , where , and are positive integers and is not divisible by the square of any prime number. Find .
Solution:
Problem 15: Let be the probability that, in the process of repeatedly flipping a fair coin, one will encounter a run of heads before one encounters a run of tails. Given that can be written in the form , where and are relatively prime positive integers, find .
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions