¶ 2006 AIME II Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2006 AIME II problems here.
Discussion Forum
Engage in discussion about the 2006 AIME II math contest by visiting Random Math AIME II 2006 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2006 AIME II problems, please refer below:
Problem 1: In convex hexagon , all six sides are congruent, and are right angles, and , and are congruent. The area of the hexagonal region is . Find .
Solution:
Problem 2: The lengths of the sides of a triangle with positive area are , and , where is a positive integer. Find the number of possible values for .
Solution:
Problem 3: Let be the product of the first positive odd integers.Find the largest integer such that is divisible by .
Solution:
Problem 4: Let be a permutation of for which
An example of such a permutation is . Find the number of such permutations.
Solution:
Problem 5: When rolling a certain unfair six-sided die with faces numbered , and , the probability of obtaining face is greater than , the probability of obtaining the face opposite face is less than , the probability of obtaining each of the other faces is , and the sum of the numbers on each pair of opposite faces is . When two such dice are rolled, the probability of obtaining a sum of is . Given that the probability of obtaining face is , where and are relatively prime positive integers, find .
Solution:
Problem 6: Square has sides of length . Points and are on and , respectively, so that is equilateral. A square with vertex has sides that are parallel to those of and a vertex on . The length of a side of this smaller square is , where , and are positive integers and is not divisible by the square of any prime. Find .
Solution:
Problem 7: Find the number of ordered pairs of positive integers such that and neither nor has a zero digit.
Solution:
Problem 8: There is an unlimited supply of congruent equilateral triangles made of colored paper. Each triangle is a solid color with the same color on both sides of the paper. A large equilateral triangle is constructed from four of these paper triangles as shown. Two large triangles are considered distinguishable if it is not possible to place one on the other,using translations, rotations, and/or reflections, so that their corresponding small triangles are of the same color. Given that there are six different colors of triangles from which to choose, how many distinguishable large equilateral triangles can be constructed?
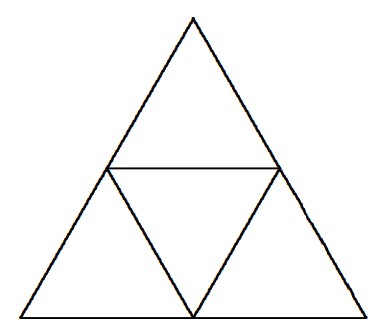
Solution:
Problem 9: Circles , and have their centers at , and , and have radii , and , respectively. Line is a common internal tangent to and and has a positive slope, and line is a common internal tangent to and and has a negative slope. Given that lines and intersect at , and that , where , and are positive integers and is not divisible by the square of any prime, find .
Solution:
Problem 10: Seven teams play a soccer tournament in which each team plays every other team exactly once. No ties occur, each team has a chance of winning each game it plays, and the outcomes of the games are independent. In each game, the winner is awarded point and the loser gets points. The total points are accumulated to decide the ranks of the teams. In the first game of the tournament, team beats team . The probability that team finishes with more points than team is , where and are relatively prime positive integers. Find .
Solution:
Problem 11: A sequence is defined as follows: , and, for all positive integers , . Given that , and , find the remainder when is divided by .
Solution:
Problem 12: Equilateral is inscribed in a circle of radius . Extend through to point so that , and extend through to point so that . Through , draw a line parallel to , and through , draw a line parallel to . Let be the intersection of and . Let be the point on the circle that is collinear with and and distinct from . Given that the area of can be expressed in the form , where , and are positive integers, and are relatively prime, and is not divisible by the square of any prime, find .
Solution:
Problem 13: How many integers less than can be written as the sum of consecutive positive odd integers for exactly values of
Solution:
Problem 14: Let be the sum of the reciprocals of the nonzero digits of the integers from to , inclusive. Find the smallest positive integer for which is an integer.
Solution:
Problem 15: Given that , and are real numbers that satisfy
and that , where and are positive integers, and is not divisible by the square of any prime, find .
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions