¶ 2006 AIME I Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2006 AIME I problems here.
Discussion Forum
Engage in discussion about the 2006 AIME I math contest by visiting Random Math AIME I 2006 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2006 AIME I problems, please refer below:
Problem 1: In quadrilateral is a right angle, diagonal is perpendicular to , , and . Find the perimeter of .
Solution:
Problem 2: Let set be a 90 -element subset of , and let be the sum of the elements of . Find the number of possible values of .
Solution:
Problem 3: Find the least positive integer such that when its leftmost digit is deleted, the resulting integer is of the original integer.
Solution:
Problem 4: Let be the number of consecutive 's at the right end of the decimal representation of the product . Find the remainder when is divided by .
Solution:
Problem 5: The number
can be written as , where , and are positive integers. Find .
Solution:
Problem 6: Let be the set of real numbers that can be represented as repeating decimals of the form where are distinct digits. Find the sum of the elements of .
Solution:
Problem 7: An angle is drawn on a set of equally spaced parallel lines as shown. The ratio of the area of shaded region to the area of shaded region is . Find the ratio of the area of shaded region to the area of shaded region .
.jpg)
Solution:
Problem 8: Hexagon is divided into five rhombuses, , and , as shown. Rhombuses , and are congruent, and each has area . Let be the area of rhombus . Given that is a positive integer, find the number of possible values for .
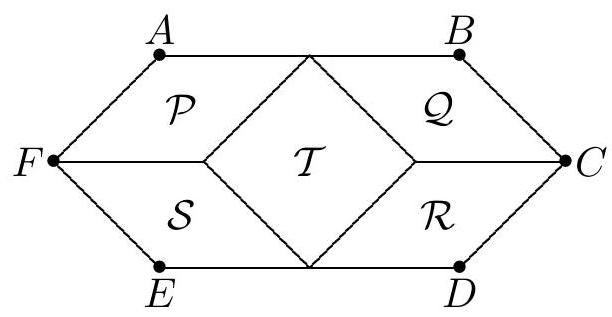
Solution:
Problem 9: The sequence is geometric with and common ratio , where and are positive integers. Given that , find the number of possible ordered pairs .
Solution:
Problem 10: Eight circles of diameter are packed in the first quadrant of the coordinate plane as shown. Let region be the union of the eight circular regions. Line , with slope , divides into two regions of equal area. Line 's equation can be expressed in the form , where , and are positive integers whose greatest common divisor is . Find .
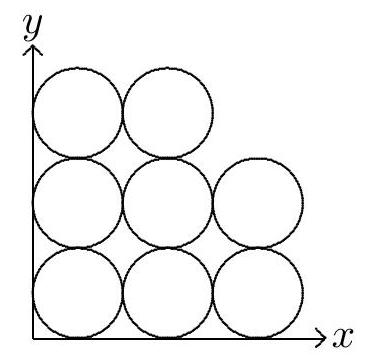
Solution:
Problem 11: A collection of cubes consists of one cube with edge-length for each integer . A tower is to be built using all cubes according to the rules:
- Any cube may be the bottom cube in the tower.
- The cube immediately on top of a cube with edge-length must have edge-length at most .
Let be the number of different towers that can be constructed. What is the remainder when is divided by
Solution:
Problem 12: Find the sum of the values of such that , where is measured in degrees and .
Solution:
Problem 13: For each even positive integer , let denote the greatest power of that divides . For example, and . For each positive integer , let . Find the greatest integer less than 1000 such that is a perfect square.
Solution:
Problem 14: A tripod has three legs each of length feet. When the tripod is set up, the angle between any pair of legs is equal to the angle between any other pair, and the top of the tripod is feet from the ground. In setting up the tripod, the lower foot of one leg breaks off. Let be the height in feet of the top of the tripod from the ground when the broken tripod is set up. Then can be written in the form , where and are positive integers and is not divisible by the square of any prime. Find . (The notation denotes the greatest integer that is less than or equal to .)
Solution:
Problem 15: Given that a sequence satisfies and for all integers , find the minimum possible value of .
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions