¶ 2021 AIME I Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2021 AIME I problems here.
Discussion Forum
Engage in discussion about the 2021 AIME I math contest by visiting Random Math AIME I 2021 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2021 AIME I problems, please refer below:
Problem 1: Zou and Chou are practicing their -meter sprints by running races against each other. Zou wins the first race, and after that, the probability that one of them wins a race is if they won the previous race but only if they lost the previous race. The probability that Zou will win exactly of the races is , where and are relatively prime positive integers. Find .
Solution:
Problem 2: In the diagram below, is a rectangle with side lengths and , and is a rectangle with side lengths and . The area of the shaded region common to the interiors of both rectangles is , where and are relatively prime positive integers. Find .
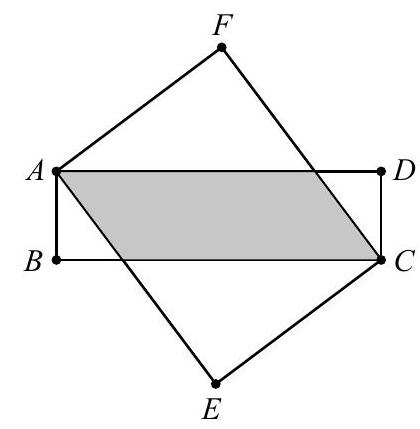
Solution:
Problem 3: Find the number of positive integers less than that can be expressed as the difference of two integral powers of .
Solution:
Problem 4: Find the number of ways identical coins can be separated into three nonempty piles so that there are fewer coins in the first pile than in the second pile and fewer coins in the second pile than in the third pile.
Solution:
Problem 5: Call a three-term strictly increasing arithmetic sequence of integers special if the sum of the squares of the three terms equals the product of the middle term and the square of the common difference. Find the sum of the third terms of all special sequences.
Solution:
Problem 6: Segments , and are edges of a cube and segment is a diagonal through the center of the cube. Point satisfies , and . Find .
Solution:
Problem 7: Find the number of pairs of positive integers with such that there exists a real number satisfying
Solution:
Problem 8: Find the number of integers such that the equation
has distinct real solutions.
Solution:
Problem 9: Let be an isosceles trapezoid with and . Suppose that the distances from to the lines , and are , and , respectively. Let be the area of . Find .
Solution:
Problem 10: Consider the sequence of positive rational numbers defined by and for , if for relatively prime positive integers and , then
Determine the sum of all positive integers such that the rational number can be written in the form for some positive integer .
Solution:
Problem 11: Let be a cyclic quadrilateral with , and . Let and be the feet of the perpendiculars from and , respectively, to line , and let and be the feet of the perpendiculars from and , respectively, to line . The perimeter of is , where and are relatively prime positive integers. Find .
Solution:
Problem 12: Let be a dodecagon (-gon). Three frogs initially sit at , and . At the end of each minute, simultaneously each of the three frogs jumps to one of the two vertices adjacent to its current position, chosen randomly and independently with both choices being equally likely. All three frogs stop jumping as soon as two frogs arrive at the same vertex at the same time. The expected number of minutes until the frogs stop jumping is , where and are relatively prime positive integers. Find .
Solution:
Problem 13: Circles and with radii and , respectively, intersect at distinct points and . A third circle is externally tangent to both and . Suppose line intersects at two points and such that the measure of minor arc is . Find the distance between the centers of and .
Solution:
Problem 14: For any positive integer denotes the sum of the positive integer divisors of . Let be the least positive integer such that is divisible by for all positive integers . Find the sum of the prime factors in the prime factorization of .
Solution:
Problem 15: Let be the set of positive integers such that the two parabolas
intersect in four distinct points, and these four points lie on a circle with radius at most . Find the sum of the least element of and the greatest element of .
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions