¶ 2002 AMC 10A Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2002 AMC 10A problems here.
Discussion Forum
Engage in discussion about the 2002 AMC 10A math contest by visiting Random Math AMC 10A 2002 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2002 AMC 10A problems, please refer below:
Problem 1: The ratio is closest to which of the following numbers?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: For the nonzero numbers , and , define
Find .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: According to the standard convention for exponentiation,
If the order in which the exponentiations are performed is changed, how many other values are possible?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: For how many positive integers does there exist at least one positive integer such that
Answer Choices:
A.
B.
C.
D.
E. infinitely many
Solution:
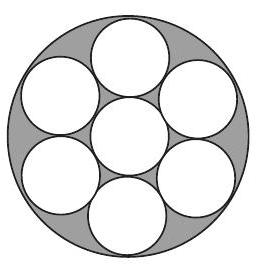
Problem 5: Each of the small circles in the figure has radius one. The innermost circle is tangent to the six circles that surround it, and each of those circles is tangent to the large circle and to its small-circle neighbors. Find the area of the shaded region.
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: Cindy was asked by her teacher to subtract from a certain number and then divide the result by . Instead, she subtracted and then divided the result by , giving an answer of . What would her answer have been had she worked the problem correctly?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: If an of on circle has the same length as an arc of on circle , then the ratio of the area of circle to the area of circle is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Betsy designed a flag using blue triangles, small white squares, and a red center square, as shown. Let be the total area of the blue triangles, the total area of the white squares, and the area of the red square. Which of the following is correct?

Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: Suppose , and are three numbers for which and . The average of the three numbers , and is
Answer Choices:
A.
B.
C.
D.
E. not uniquely determined
Solution:
Problem 10: Compute the sum of all the roots of .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: Jamal wants to store computer files on floppy disks, each of which has a capacity of megabytes . Three of his files require of memory each, more require each, and the remaining require each. No file can be split between floppy disks. What is the minimal number of floppy disks that will hold all the files?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: Mr. Earl E. Bird leaves his house for work at exactly A.M. every morning. When he averages miles per hour, he arrives at his workplace three minutes late. When he averages miles per hour, he arrives three minutes early. At what average speed, in miles per hour, should Mr. Bird drive to arrive at his workplace precisely on time?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: The sides of a triangle have lengths of , and . Find the length of the shortest altitude.
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Both roots of the quadratic equation are prime numbers. The number of possible values of is
Answer Choices:
A.
B.
C.
D.
E. more than four
Solution:
Problem 15: The digits , and are used to form four two-digit prime numbers, with each digit used exactly once. What is the sum of these four primes?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: If , then is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Sarah pours four ounces of coffee into an eight-ounce cup and four ounces of cream into a second cup of the same size. She then transfers half the coffee from the first cup to the second and, after stirring thoroughly, transfers half the liquid in the second cup back to the first. What fraction of the liquid in the first cup is now cream?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: A cube is formed by gluing together standard cubical dice. (On a standard die, the sum of the numbers on any pair of opposite faces is .) The smallest possible sum of all the numbers showing on the surface of the cube is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: Spot's doghouse has a regular hexagonal base that measures one yard on each side. He is tethered to a vertex with a two-yard rope. What is the area, in square yards, of the region outside the doghouse that Spot can reach?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
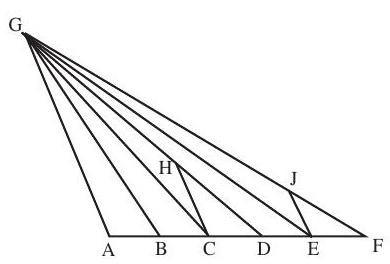
Problem 20: Points , and lie, in that order, on , dividing it into five segments, each of length . Point is not on line . Point lies on , and point lies on . The line segments , and are parallel. Find .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: The mean, median, unique mode, and range of a collection of eight integers are all equal to . The largest integer that can be an element of this collection is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: A set of tiles numbered through is modified repeatedly by the following operation: remove all tiles numbered with a perfect square, and renumber the remaining tiles consecutively starting with . How many times must the operation be performed to reduce the number of tiles in the set to one?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: Points , and lie on a line, in that order, with and . Point is not on the line, and . The perimeter of is twice the perimeter of . Find .
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Tina randomly selects two distinct numbers from the set , and Sergio randomly selects a number from the set . The probability that Sergio's number is larger than the sum of the two numbers chosen by Tina is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
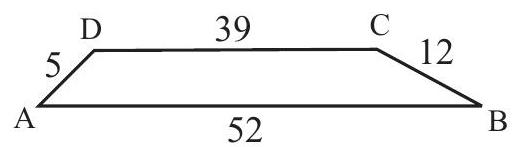
Problem 25: In trapezoid with bases and , we have , , and . The area of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions