¶ 2002 AMC 10B Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2002 AMC 10B problems here.
Discussion Forum
Engage in discussion about the 2002 AMC 10B math contest by visiting Random Math AMC 10B 2002 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2002 AMC 10B problems, please refer below:
Problem 1: The ratio is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: For the nonzero numbers , and , define
Find .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: The arithmetic mean of the nine numbers in the set is a -digit number , all of whose digits are distinct. The number does not contain the digit
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: What is the value of
when
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Circles of radius and are externally tangent and are circumscribed by a third circle, as shown in the figure. Find the area of the shaded region.
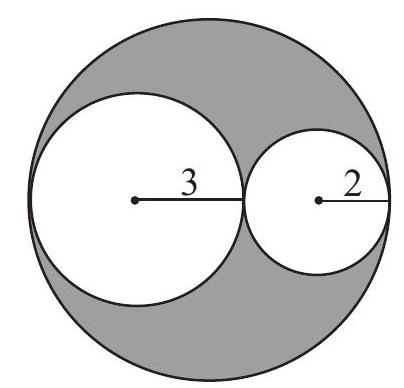
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: For how many positive integers is a prime number?
Answer Choices:
A. none
B. one
C. two
D. more than two, but finitely many
E. infinitely many
Solution:
Problem 7: Let be a positive integer such that is an integer. Which of the following statements is not true:
Answer Choices:
A. divides
B. divides
C. divides
D. divides
E.
Solution:
Problem 8: Suppose July of year has five Mondays. Which of the following must occur five times in August of year (Note: Both months have days.)
Answer Choices:
A. Monday
B. Tuesday
C. Wednesday
D. Thursday
E. Friday
Solution:
Problem 9: Using the letters , and , we can form five-letter words. If these words are arranged in alphabetical order, then the word occupies position
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Suppose that and are nonzero real numbers, and that the equation has solutions and . Then the pair is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: The product of three consecutive positive integers is times their sum. What is the sum of their squares?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: For which of the following values of does the equation have no solution for
Answer Choices:
A.
B.
C.
D.
E. }
Solution:
Problem 13: Find the value(s) of such that is true for all values of .
Answer Choices:
A.
B. or
C. or
D.
E. or
Solution:
Problem 14: The number is the square of a positive integer . In decimal representation, the sum of the digits of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: The positive integers , and are all prime numbers. The sum of these four primes is
Answer Choices:
A. even
B. divisible by
C. divisible by
D. divisible by
E. prime
Solution:
Problem 16: For how many integers is the square of an integer?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: A regular octagon has sides of length two. Find the area of .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: Four distinct circles are drawn in a plane. What is the maximum number of points where at least two of the circles intersect?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: Suppose that Suppose that is an arithmetic sequence with
and
What is the value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Let , and be real numbers such that and . Then is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Andy's lawn has twice as much area as Beth's lawn and three times as much area as Carlos' lawn. Carlos' lawn mower cuts half as fast as Beth's mower and one third as fast as Andy's mower. If they all start to mow their lawns at the same time, who will finish first?
Answer Choices:
A. Andy
B. Beth
C. Carlos
D. Andy and Carlos tie for first.
E. All three tie.
Solution:
Problem 22: Let be a right-angled triangle with . Let and be the midpoints of legs and , respectively. Given that and , find .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: Let be a sequence of integers such that and , for all positive integers and . Then is
Answer Choices:
A.
B.
C.
D.
E. }
Solution:
Problem 24: Riders on a Ferris wheel travel in a circle in a vertical plane. A particular wheel has radius feet and revolves at the constant rate of one revolution per minute. How many seconds does it take a rider to travel from the bottom of the wheel to a point vertical feet above the bottom?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: When is appended to a list of integers, the mean is increased by . When is appended to the enlarged list, the mean of the enlarged list is decreased by . How many integers were in the original list?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions