¶ 2003 AMC 10B Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2003 AMC 10B problems here.
Discussion Forum
Engage in discussion about the 2003 AMC 10B math contest by visiting Random Math AMC 10B 2003 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2003 AMC 10B problems, please refer below:
Problem 1: Which of the following is the same as
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: Al gets the disease algebritis and must take one green pill and one pink pill each day for two weeks. A green pill costs more than a pink pill, and Al's pills cost a total of for the two weeks. How much does one green pill cost?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: The sum of consecutive even integers is less than the sum of the first consecutive odd counting numbers. What is the smallest of the even integers?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Rose fills each of the rectangular regions of her rectangular flower bed with a different type of flower. The lengths, in feet, of the rectangular regions in her flower bed are as shown in the figure. She plants one flower per square foot in each region. Asters cost each, begonias each, cannas each, dahlias each, and Easter lilies each. What is the least possible cost, in dollars, for her garden?
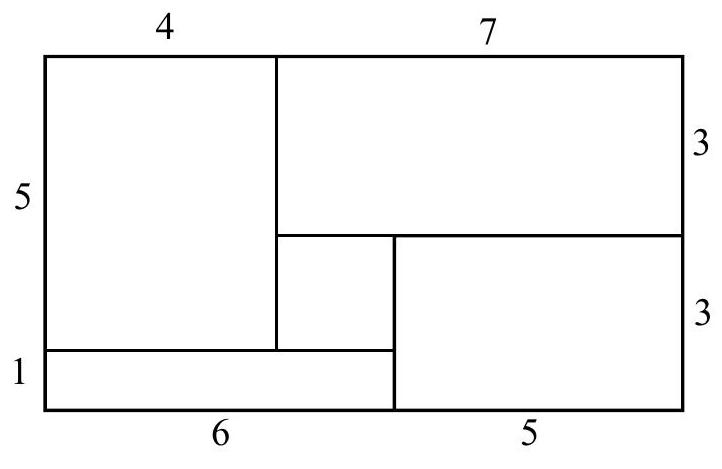
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Moe uses a mower to cut his rectangular -foot by -foot lawn. The swath he cuts is inches wide, but he overlaps each cut by inches to make sure that no grass is missed. He walks at the rate of feet per hour while pushing the mower. Which of the following is closest to the number of hours it will take Moe to mow his lawn?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: Many television screens are rectangles that are measured by the length of their diagonals. The ratio of the horizontal length to the height in a standard television screen is . The horizontal length of a "-inch" television screen is closest, in inches, to which of the following?
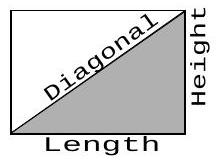
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: The symbolism denotes the largest integer not exceeding . For example, , and . Compute
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: The second and fourth terms of a geometric sequence are and . Which of the following is a possible first term?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: Find the value of that satisfies the equation
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Nebraska, the home of the AMC, changed its license plate scheme. Each old license plate consisted of a letter followed by four digits. Each new license plate consists of three letters followed by three digits. By how many times is the number of possible license plates increased?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: A line with slope intersects a line with slope at the point . What is the distance between the -intercepts of these two lines?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: Al, Betty, and Clare split among them to be invested in different ways. Each begins with a different amount. At the end of one year they have a total of . Betty and Clare have both doubled their money, whereas Al has managed to lose . What was Al's original portion?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Let denote the sum of the digits of the positive integer . For example, and . For how many two-digit values of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Given that , where both and are positive integers, find the smallest possible value for .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: There are players in a singles tennis tournament. The tournament is single elimination, meaning that a player who loses a match is eliminated. In the first round, the strongest players are given a bye, and the remaining players are paired off to play. After each round, the remaining players play in the next round. The match continues until only one player remains unbeaten. The total number of matches played is
Answer Choices:
A. a prime number
B. divisible by
C. divisible by
D. divisible by
E. divisible by
Solution:
Problem 16: A restaurant offers three desserts, and exactly twice as many appetizers as main courses. A dinner consists of an appetizer, a main course, and a dessert. What is the least number of main courses that the restaurant should offer so that a customer could have a different dinner each night in the year
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: An ice cream cone consists of a sphere of vanilla ice cream and a right circular cone that has the same diameter as the sphere. If the ice cream melts, it will exactly fill the cone. Assume that the melted ice cream occupies of the volume of the frozen ice cream. What is the ratio of the cone's height to its radius? (Note: A cone with radius and height has volume , and a sphere with radius has volume .)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: What is the largest integer that is a divisor of
for all positive even integers
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: Three semicircles of radius are constructed on diameter of a semicircle of radius . The centers of the small semicircles divide into four line segments of equal length, as shown. What is the area of the shaded region that lies within the large semicircle but outside the smaller semicircles?
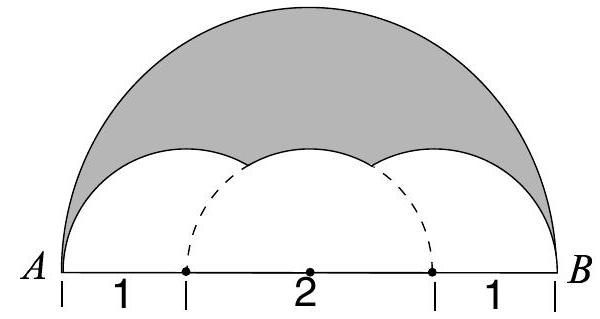
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: In rectangle and . Points and are on so that and . Lines and intersect at . Find the area of .
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: A bag contains two red beads and two green beads. You reach into the bag and pull out a bead, replacing it with a red bead regardless of the color you pulled out. What is the probability that all beads in the bag are red after three such replacements?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: A clock chimes once at minutes past each hour and chimes on the hour according to the hour. For example, at PM there is one chime and at noon and midnight there are twelve chimes. Starting at AM on February , , on what date will the chime occur?
Answer Choices:
A. March
B. March
C. March
D. March
E. March
Solution:
Problem 23: A regular octagon has an area of one square unit. What is the area of the rectangle
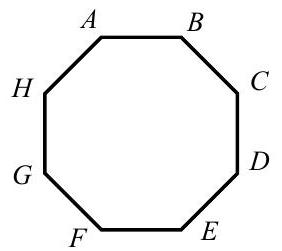
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: The first four terms in an arithmetic sequence are , and , in that order. What is the fifth term?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: How many distinct four-digit numbers are divisible by and have as their last two digits?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions