¶ 2004 AMC 10A Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2004 AMC 10A problems here.
Discussion Forum
Engage in discussion about the 2004 AMC 10A math contest by visiting Random Math AMC 10A 2004 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2004 AMC 10A problems, please refer below:
Problem 1: You and five friends need to raise in donations for a charity, dividing the fundraising equally. How many dollars will each of you need to raise?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: For any three real numbers , , and , with , the operation is defined by:
What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: Alicia earns per hour, of which is deducted to pay local taxes. How many cents per hour of Alicia's wages are used to pay local taxes?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: What is the value of if ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: A set of three points is chosen randomly from the grid shown. Each three-point set has the same probability of being chosen. What is the probability that the points lie on the same straight line?

Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: Bertha has daughters and no sons. Some of her daughters have daughters, and the rest have none. Bertha has a total of daughters and granddaughters, and no great-granddaughters. How many of Bertha's daughters and granddaughters have no daughters?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: A grocer stacks oranges in a pyramid-like stack whose rectangular base is oranges by oranges. Each orange above the first level rests in a pocket formed by four oranges in the level below. The stack is completed by a single row of oranges. How many oranges are in the stack?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: A game is played with tokens according to the following rule. In each round, the player with the most tokens gives one token to each of the other players and also places one token into a discard pile. The game ends when some player runs out of tokens. Players , and start with , and tokens, respectively. How many rounds will there be in the game?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: In the Figure, and are right angles, , and and intersect at . What is the difference between the areas of and
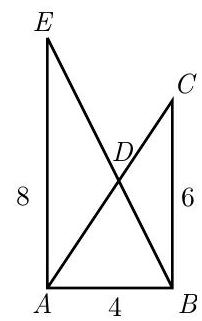
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Coin is flipped three times and coin is flipped four times. What is the probability that the number of heads obtained from flipping the two fair coins is the same?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: A company sells peanut butter in cylindrical jars. Marketing research suggests that using wider jars will increase sales. If the diameter of the jars is increased by without altering the volume, by what percent must the height be decreased?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: Henry's Hamburger Heaven o ers its hamburgers with the following condiments: ketchup, mustard, mayonnaise, tomato, lettuce, pickles, cheese, and onions. A customer can choose one, two, or three meat patties, and any collection of condiments. How many different kinds of hamburgers can be ordered?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: At a party, each man danced with exactly three women and each woman danced with exactly two men. Twelve men attended the party. How many women attended the party?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: The average value of all the pennies, nickels, dimes, and quarters in Paula's purse is cents. If she had one more quarter, the average value would be cents. How many dimes does she have in her purse?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: Given that and , what is the largest possible value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: The grid shown contains a collection of squares with sizes from to . How many of these squares contain the black center square?

Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Brenda and Sally run in opposite directions on a circular track, starting at diametrically opposite points. They first meet after Brenda has run meters. They next meet after Sally has run meters past their first meeting point. Each girl runs at a constant speed. What is the length of the track in meters?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: A sequence of three real numbers forms an arithmetic progression with a first term of . If is added to the second term and is added to the third term, the three resulting numbers form a geometric progression. What is the smallest possible value for the third term of the geometric progression?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: A white cylindrical silo has a diameter of feet and a height of feet. A red stripe with a horizontal width of feet is painted on the silo, as shown, making two complete revolutions around it. What is the area of the stripe in square feet?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Points and are located on square so that is equilateral. What is the ratio of the area of to that of
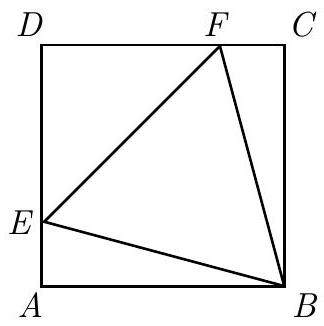
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Two distinct lines pass through the center of three concentric circles of radii , , and . The area of the shaded region in the diagram is of the area of the unshaded region. What is the radian measure of the acute angle formed by the two lines? (Note: radians is degrees.)
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Square has side length . A semicircle with diameter is constructed inside the square, and the tangent to the semicircle from intersects side at . What is the length of
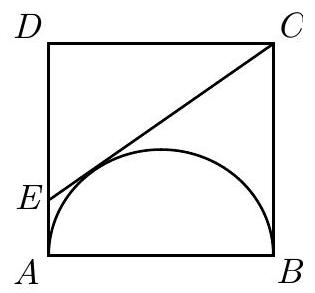
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: Circles , and are externally tangent to each other and internally tangent to circle . Circles and are congruent. Circle has radius and passes through the center of . What is the radius of circle
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Let , be a sequence with the following properties.
(i) , and
(ii) for any positive integer .
What is the value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Three mutually tangent spheres of radius rest on a horizontal plane. A sphere of radius rests on them. What is the distance from the plane to the top of the larger sphere?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions