¶ 2005 AMC 10B Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2005 AMC 10B problems here.
Discussion Forum
Engage in discussion about the 2005 AMC 10B math contest by visiting Random Math AMC 10B 2005 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2005 AMC 10B problems, please refer below:
Problem 1: A scout troop buys candy bars at a price of five for . They sell all the candy bars at a price of two for . What was their profit, in dollars?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: A positive number has the property that of is . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: A gallon of paint is used to paint a room. One third of the paint is used on the first day. On the second day, one third of the remaining paint is used. What fraction of the original amount of paint is available to use on the third day?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: For real numbers and , define . What is the value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Brianna is using part of the money she earned on her weekend job to buy several equally-priced CDs. She used one fifth of her money to buy one third of the CDs. What fraction of her money will she have left after she buys all the CDs?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: At the beginning of the school year, Lisa's goal was to earn an on at least of her quizzes for the year. She earned an on of the first quizzes. If she is to achieve her goal, on at most how many of the remaining quizzes can she earn a grade lower than an
Answer Choices:
A.
B.
C. $ 3$
D.
E.
Solution:
Problem 7: A circle is inscribed in a square, then a square is inscribed in this circle, and finally, a circle is inscribed in this square. What is the ratio of the area of the smaller circle to the area of the larger square?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: An -foot by -foot floor is tiled with square tiles of size foot by foot. Each tile has a pattern consisting of four white quarter circles of radius foot centered at each corner of the tile. The remaining portion of the tile is shaded. How many square feet of the floor are shaded?
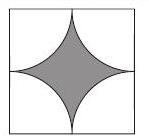
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: One fair die has faces and another has faces . The dice are rolled and the numbers on the top faces are added. What is the probability that the sum will be odd?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
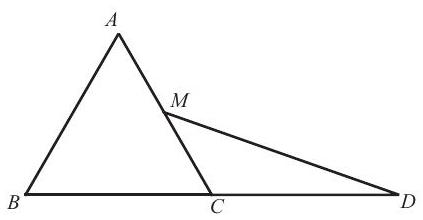
Problem 10: In , we have and . Suppose that is a point on line such that lies between and and . What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: The first term of a sequence is . Each succeeding term is the sum of the cubes of the digits of the previous term. What is the term of the sequence?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: Twelve fair dice are rolled. What is the probability that the product of the numbers on the top faces is prime?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: How many numbers between and are integer multiples of or but not
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Equilateral has side length is the midpoint of , and is the midpoint of . What is the area of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: An envelope contains eight bills: ones, fives, tens, and twenties. Two bills are drawn at random without replacement. What is the probability that their sum is or more?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: The quadratic equation has roots that are twice those of , and none of , and is zero. What is the value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Suppose that ,,, and . What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: All of David's telephone numbers have the form -abc-defg, where , , and are distinct digits and in increasing order, and none is either or . How many different telephone numbers can David have?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: On a certain math exam, of the students got points, got points, got points, got points, and the rest got points. What is the difference between the mean and the median score on this exam?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: What is the average (mean) of all -digit numbers that can be formed by using each of the digits , and exactly once?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Forty slips are placed into a hat, each bearing a number , or , with each number entered on four slips. Four slips are drawn from the hat at random and without replacement. Let be the probability that all four slips bear the same number. Let be the probability that two of the slips bear a number and the other two bear a number . What is the value of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: For how many positive integers less than or equal to is evenly divisible by ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: In trapezoid we have parallel to as the midpoint of , and as the midpoint of . The area of is twice the area of . What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Let and be two-digit integers such that is obtained by reversing the digits of . The integers and satisfy for some positive integer . What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: A subset of the set of integers from to , inclusive, has the property that no two elements of sum to . What is the maximum possible number of elements in
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions