¶ 2005 AMC 10A Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2005 AMC 10A problems here.
Discussion Forum
Engage in discussion about the 2005 AMC 10A math contest by visiting Random Math AMC 10A 2005 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2005 AMC 10A problems, please refer below:
Problem 1: While eating out, Mike and Joe each tipped their server . Mike tipped of his bill and Joe tipped of his bill. What was the difference, in dollars, between their bills?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: For each pair of real numbers , define the operation as
What is the value of ?
Answer Choices:
A.
B.
C.
D.
E. This value is not defined.
Solution:
Problem 3: The equations and have the same solution . What is the value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: A rectangle with a diagonal of length is twice as long as it is wide. What is the area of the rectangle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: A store normally sells windows at each. This week the store is offering one free window for each purchase of four. Dave needs seven windows and Doug needs eight windows. How many dollars will they save if they purchase the windows together rather than separately?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: The average (mean) of numbers is , and the average of other numbers is . What is the average of all numbers?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: Josh and Mike live miles apart. Yesterday Josh started to ride his bicycle toward Mike's house. A little later Mike started to ride his bicycle toward Josh's house. When they met, Josh had ridden for twice the length of time as Mike and at four-fifths of Mike's rate. How many miles had Mike ridden when they met?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
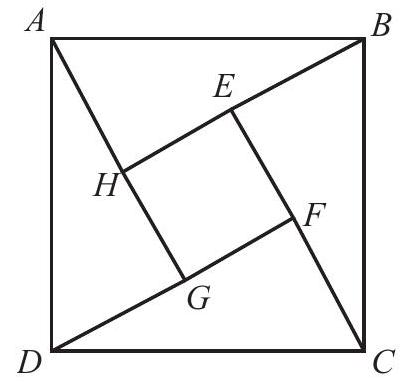
Problem 8: In the figure, the length of side of square is is between and , and . What is the the area of the inner square ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: Three tiles are marked and two other tiles are marked . The five tiles are randomly arranged in a row. What is the probability that the arrangement reads ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: There are two values of for which the equation has only one solution for . What is the sum of those values of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: A wooden cube units on a side is painted red on all six faces and then cut into unit cubes. Exactly one-fourth of the total number of faces of the unit cubes are red. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: The figure shown is called a trefoil and is constructed by drawing circular sectors about sides of the congruent equilateral triangles. What is the area of a trefoil whose horizontal base has length ?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: How many positive integers satisfy the following condition:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: How many three-digit numbers satisfy the property that the middle digit is the average of the first and the last digits?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: How many positive cubes divide ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: The sum of the digits of a two-digit number is subtracted from the number. The units digit of the result is . How many two-digit numbers have this property?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
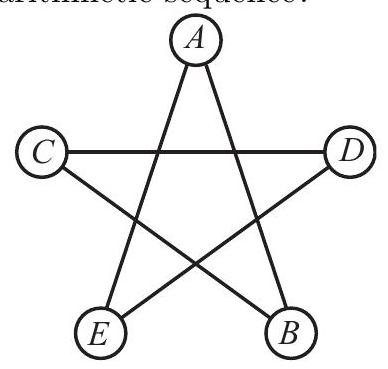
Problem 17: In the five-sided star shown, the letters , and are replaced by the numbers , and , although not necessarily in this order. The sums of the numbers at the ends of the line segments , and form an arithmetic sequence, although not necessarily in this order. What is the middle term of the arithmetic sequence?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: Team and team play a series. The first team to win three games wins the series. Each team is equally likely to win each game, there are no ties, and the outcomes of the individual games are independent. If team wins the second game and team wins the series, what is the probability that team wins the first game?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
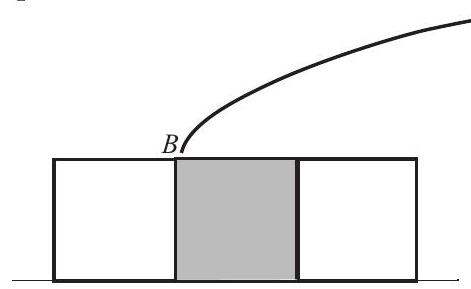
Problem 19: Three one-inch squares are placed with their bases on a line. The center square is lifted out and rotated , as shown. Then it is centered and lowered into its original location until it touches both of the adjoining squares. How many inches is the point from the line on which the bases of the original squares were placed?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: An equiangular octagon has four sides of length and four sides of length , arranged so that no two consecutive sides have the same length. What is the area of the octagon?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: For how many positive integers does evenly divide ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Let be the set of the smallest positive multiples of , and let be the set of the smallest positive multiples of . How many elements are common to and ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: Let be a diameter of a circle and be a point on with . Let and be points on the circle such that and is a second diameter. What is the ratio of the area of to the area of ?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: For each positive integer , let denote the greatest prime factor of . For how many positive integers is it true that both and ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: In we have , , and . Points and are on and respectively, with and . What is the ratio of the area of triangle to the area of the quadrilateral ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions