¶ 2010 AMC 10A Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2010 AMC 10A problems here.
Discussion Forum
Engage in discussion about the 2010 AMC 10A math contest by visiting Random Math AMC 10A 2010 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2010 AMC 10A problems, please refer below:
Problem 1: Mary's top book shelf holds five books with the following widths, in centimeters: , and . What is the average book width, in centimeters?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: Four identical squares and one rectangle are placed together to form one large square as shown. The length of the rectangle is how many times as large as its width?
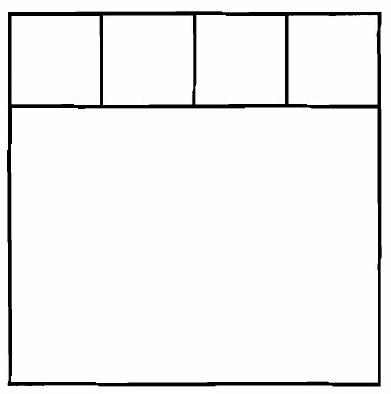
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: Tyrone had marbles and Eric had marbles. Tyrone then gave some of his marbles to Eric so that Tyrone ended with twice as many marbles as Eric. How many marbles did Tyrone give to Eric?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: A book that is to be recorded onto compact discs takes minutes to read aloud. Each disc can hold up to minutes of reading. Assume that the smallest possible number of discs is used and that each disc contains the same length of reading. How many minutes of reading will each disc contain?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: The area of a circle whose circumference is is . What is the value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: For positive numbers and the operation is defined as
What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: Crystal has a running course marked out for her daily run. She starts this run by heading due north for one mile. She then runs northeast for one mile, then southeast for one mile. The last portion of her run takes her on a straight line back to where she started. How far, in miles, is this last portion of her run?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Tony works hours a day and is paid per hour for each full year of his age. During a six month period Tony worked days and earned . How old was Tony at the end of the six month period?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: A palindrome, such as , is a number that remains the same when its digits are reversed. The numbers and are three-digit and four-digit palindromes, respectively. What is the sum of the digits of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Marvin had a birthday on Tuesday, May in the leap year . In what year will his birthday next fall on a Saturday?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: The length of the interval of solutions of the inequality is . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: Logan is constructing a scaled model of his town. The city's water tower stands meters high, and the top portion is a sphere that holds liters of water. Logan's miniature water tower holds liters. How tall, in meters, should Logan make his tower?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Angelina drove at an average rate of and then stopped minutes for gas. After the stop, she drove at an average rate of . Altogether she drove in a total trip time of hours including the stop. Which equation could be used to solve for the time in hours that she drove before her stop?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Triangle has . Let and be on and , respectively, such that . Let be the intersection of segments and , and suppose that is equilateral. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: In a magical swamp there are two species of talking amphibians: toads, whose statements are always true, and frogs, whose statements are always false. Four amphibians, Brian, Chris, LeRoy, and Mike live together in this swamp, and they make the following statements.
-
Brian: "Mike and I are different species."
-
Chris: "LeRoy is a frog."
-
LeRoy: "Chris is a frog."
-
Mike: "Of the four of us, at least two are toads."
How many of these amphibians are frogs?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: Nondegenerate has integer side lengths, is an angle bisector, , and . What is the smallest possible value of the perimeter?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: A solid cube has side length inches. A -inch by -inch square hole is cut into the center of each face. The edges of each cut are parallel to the edges of the cube, and each hole goes all the way through the cube. What is the volume, in cubic inches, of the remaining solid?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: Bernardo randomly picks distinct numbers from the set and arranges them in descending order to form a -digit number. Silvia randomly picks distinct numbers from the set and also arranges them in descending order to form a -digit number. What is the probability that Bernardo's number is larger than Silvia's number?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: Equiangular hexagon has side lengths and . The area of is of the area of the hexagon. What is the sum of all possible values of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: A fly trapped inside a cubical box with side length meter decides to relieve its boredom by visiting each corner of the box. It will begin and end in the same corner and visit each of the other corners exactly once. To get from a corner to any other corner, it will either fly or crawl in a straight line. What is the maximum possible length, in meters, of its path?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: The polynomial has three positive integer zeros. What is the smallest possible value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Eight points are chosen on a circle, and chords are drawn connecting every pair of points. No three chords intersect in a single point inside the circle. How many triangles with all three vertices in the interior of the circle are created?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: Each of boxes in a line contains a single red marble, and for , the box in the position also contains white marbles. Isabella begins at the first box and successively draws a single marble at random from each box, in order. She stops when she first draws a red marble. Let be the probability that Isabella stops after drawing exactly marbles. What is the smallest value of for which ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: The number obtained from the last two nonzero digits of ! is equal to . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Jim starts with a positive integer and creates a sequence of numbers. Each successive number is obtained by subtracting the largest possible integer square less than or equal to the current number until zero is reached. For example, if Jim starts with , then his sequence contains numbers:
Let be the smallest number for which Jim’s sequence has numbers. What is the units digit of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions