¶ 2015 AMC 10B Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2015 AMC 10B problems here.
Discussion Forum
Engage in discussion about the 2015 AMC 10B math contest by visiting Random Math AMC 10B 2015 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2015 AMC 10B problems, please refer below:
Problem 1: What is the value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: Marie does three equally time-consuming tasks in a row without taking breaks. She begins the first task at PM and finishes the second task at PM. When does she finish the third task?
Answer Choices:
A. PM
B. PM
C. PM
D. PM
E. PM
Solution:
Problem 3: Isaac has written down one integer two times and another integer three times. The sum of the five numbers is , and one of the numbers is . What is the other number?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Four siblings ordered an extra large pizza. Alex ate , Beth , and Cyril of the pizza. Dan got the leftovers. What is the sequence of the siblings in decreasing order of the part of the pizza they consumed?
Answer Choices:
A. Alex, Beth, Cyril, Dan
B. Beth, Cyril, Alex, Dan
C. Beth, Cyril, Dan, Alex
D. Beth, Dan, Cyril, Alex
E. Dan, Beth, Cyril, Alex
Solution:
Problem 5: David, Hikmet, Jack, Marta, Rand, and Todd were in a -person race with other people. Rand finished places ahead of Hikmet. Marta finished place behind Jack. David finished places behind Hikmet. Jack finished places behind Todd. Todd finished place behind Rand. Marta finished in th place. Who finished in th place?
Answer Choices:
A. David
B. Hikmet
C. Jack
D. Rand
E. Todd
Solution:
Problem 6: Marley practices exactly one sport each day of the week. She runs three days a week but never on two consecutive days. On Monday she plays basketball and two days later golf. She swims and plays tennis, but she never plays tennis the day after running or swimming. Which day of the week does Marley swim?
Answer Choices:
A. Sunday
B. Tuesday
C. Thursday
D. Friday
E. Saturday
Solution:
Problem 7: Consider the operation "minus the reciprocal" of, defined by . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: The letter shown below is rotated clockwise around the origin, then reflected in the -axis, and then rotated a half turn around the origin. What is the final image?
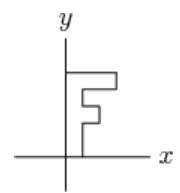
Answer Choices:
A. 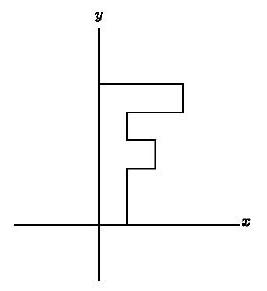
B. 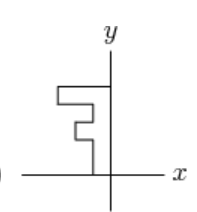
C. 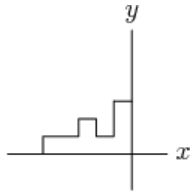
D. 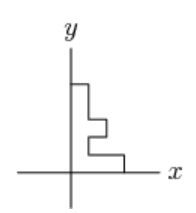
E. 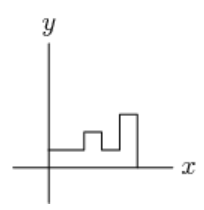
Solution:
Problem 9: The shaded region below is called a shark's fin falcata, a figure studied by Leonardo da Vinci. It is bounded by the portion of the circle of radius and center that lies in the first quadrant, the portion of the circle of radius and center that lies in the first quadrant, and the line segment from to . What is the area of the shark's fin falcata?
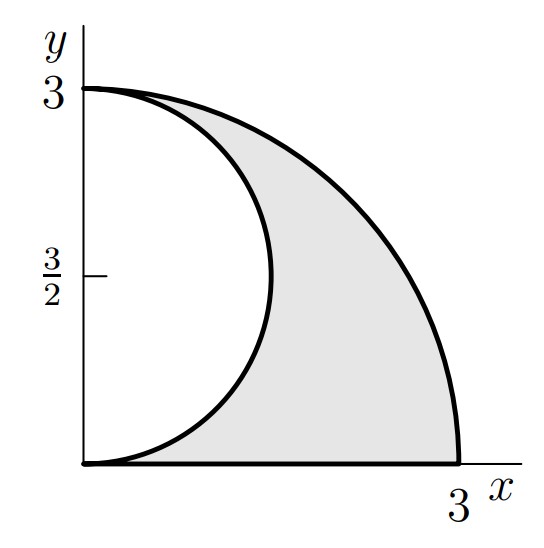
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: What are the sign and units digit of the product of all the odd negative integers strictly greater than ?
Answer Choices:
A. It is a negative number ending with a .
B. It is a positive number ending with a .
C. It is a negative number ending with a
D. It is a positive number ending with a .
E. It is a negative number ending with a
Solution:
Problem 11: Among the positive integers less than , each of whose digits is a prime number, one is selected at random. What is the probability that the selected number is prime?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: For how many integers is the point inside or on the circle of radius centered at ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: The line forms a triangle with the coordinate axes. What is the sum of the lengths of the altitudes of this triangle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Let , and be three distinct one-digit numbers. What is the maximum value of the sum of the roots of the equation ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: The town of Hamlet has people for each horse, sheep for each cow, and ducks for each person. Which of the following could not possibly be the total number of people, horses, sheep, cows, and ducks in Hamlet?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: Al, Bill, and Cal will each randomly be assigned a whole number from to , inclusive, with no two of them getting the same number. What is the probability that Al's number will be a whole number multiple of Bill's and Bill's number will be a whole number multiple of Cal's?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: The centers of the faces of the right rectangular prism shown below are joined to create an octahedron. What is the volume of the octahedron?
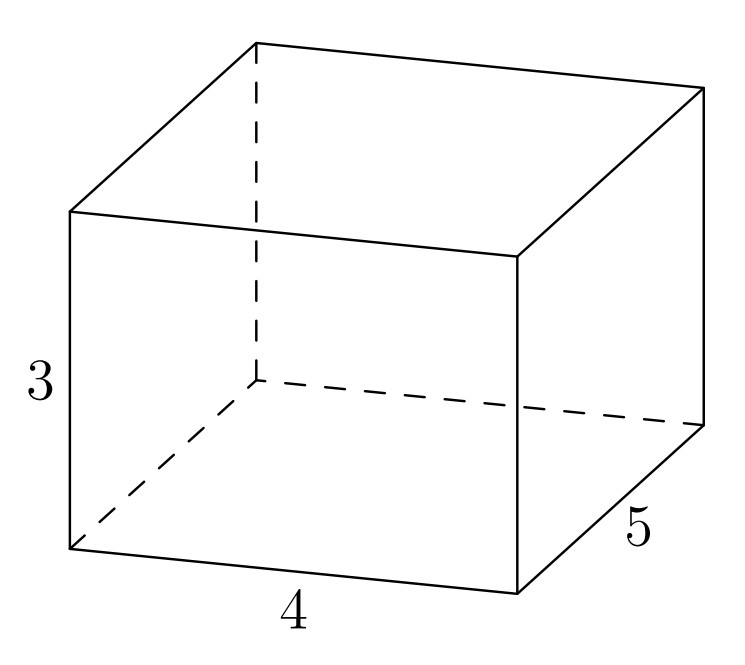
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: Johann has fair coins. He flips all the coins. Any coin that lands on tails is tossed again. Coins that land on tails on the second toss are tossed a third time. What is the expected number of coins that are now heads?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: In and . Squares and are constructed outside of the triangle. The points , and lie on a circle. What is the perimeter of the triangle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Erin the ant starts at a given corner of a cube and crawls along exactly edges in such a way that she visits every corner exactly once and then finds that she is unable to return along an edge to her starting point. How many paths are there meeting these conditions?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Cozy the Cat and Dash the Dog are going up a staircase with a certain number of steps. However, instead of walking up the steps one at a time, both Cozy and Dash jump. Cozy goes two steps up with each jump (though if necessary, he will just jump the last step). Dash goes five steps up with each jump (though if necessary, he will just jump the last steps if there are fewer than steps left). Suppose that Dash takes fewer jumps than Cozy to reach the top of the staircase. Let denote the sum of all possible numbers of steps this staircase can have. What is the sum of the digits of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: In the figure shown below, is a regular pentagon and . What is ?
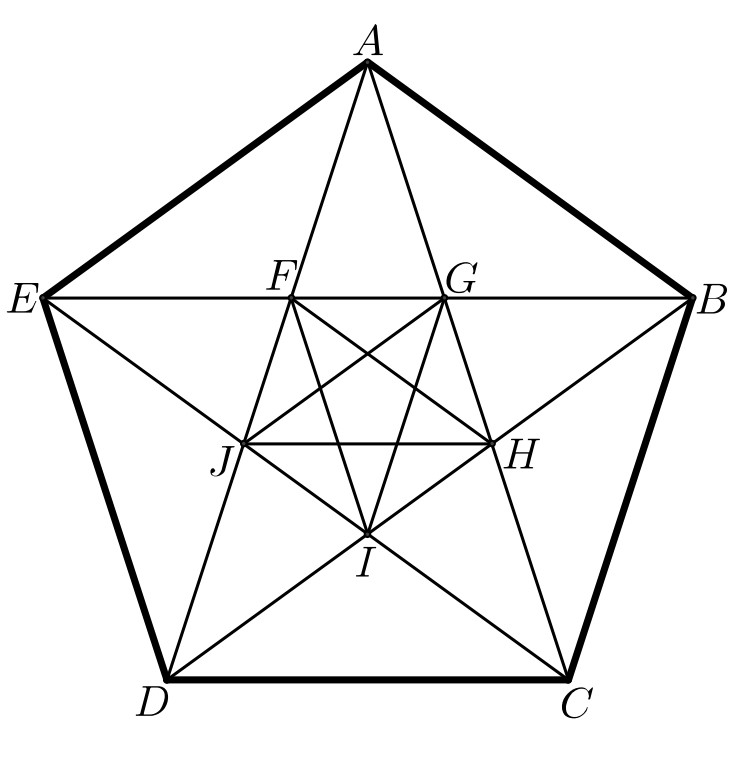
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: Let be a positive integer greater than such that the decimal representation of ends in zeros and the decimal representation of ends in zeros. Let denote the sum of the four least possible values of . What is the sum of the digits of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Aaron the ant walks on the coordinate plane according to the following rules. He starts at the origin facing to the east and walks one unit, arriving at . For , right after arriving at the point , if Aaron can turn left and walk one unit to an unvisited point , he does that. Otherwise, he walks one unit straight ahead to reach . Thus the sequence of points continues , and so in a counterclockwise spiral pattern. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: A rectangular box measures , where , and are integers and . The volume and the surface area of the box are numerically equal. How many ordered triples are possible?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions