¶ 2015 AMC 10A Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2015 AMC 10A problems here.
Discussion Forum
Engage in discussion about the 2015 AMC 10A math contest by visiting Random Math AMC 10A 2015 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2015 AMC 10A problems, please refer below:
Problem 1: What is the value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: A box contains a collection of triangular and square tiles. There are tiles in the box, containing edges total. How many square tiles are there in the box?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: Ann made a -step staircase using toothpicks as shown in the figure. How many toothpicks does she need to add to complete a -step staircase?

Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Pablo, Sofia, and Mia got some candy eggs at a party. Pablo had three times as many eggs as Sofia, and Sofia had twice as many eggs as Mia. Pablo decides to give some of his eggs to Sofia and Mia so that all three will have the same number of eggs. What fraction of his eggs should Pablo give to Sofia?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Mr. Patrick teaches math to students. He was grading tests and found that when he graded everyone's test except Payton's, the average grade for the class was . After he graded Payton's test, the class average became . What was Payton's score on the test?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: The sum of two positive numbers is times their difference. What is the ratio of the larger number to the smaller?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: How many terms are there in the arithmetic sequence ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Two years ago Pete was three times as old as his cousin Claire. Two years before that, Pete was four times as old as Claire. In how many years will the ratio of their ages be ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: Two right circular cylinders have the same volume. The radius of the second cylinder is more than the radius of the first. What is the relationship between the heights of the two cylinders?
Answer Choices:
A. The second height is less than the first
B. The first height is more than the second.
C. The second height is less than the first.
D. The first height is more than the second.
E. The second height is of the first.
Solution:
Problem 10: How many rearrangements of are there in which no two adjacent letters are also adjacent letters in the alphabet? For example, no such rearrangements could include either or .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: The ratio of the length to the width of a rectangle is . If the rectangle has diagonal of length , then the area may be expressed as for some constant . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: Points and are distinct points on the graph of
What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Claudia has coins, each of which is a -cent coin or a -cent coin. There are exactly different values that can be obtained as combinations of one or more of her coins. How many -cent coins does Claudia have?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: The diagram below shows the circular face of a clock with radius and a circular disk with radius externally tangent to the clock face at o'clock. The disk has an arrow painted on it, initially pointing in the upward vertical direction. Let the disk roll clockwise around the clock face. At what point on the clock face will the disk be tangent when the arrow is next pointing in the upward vertical direction?
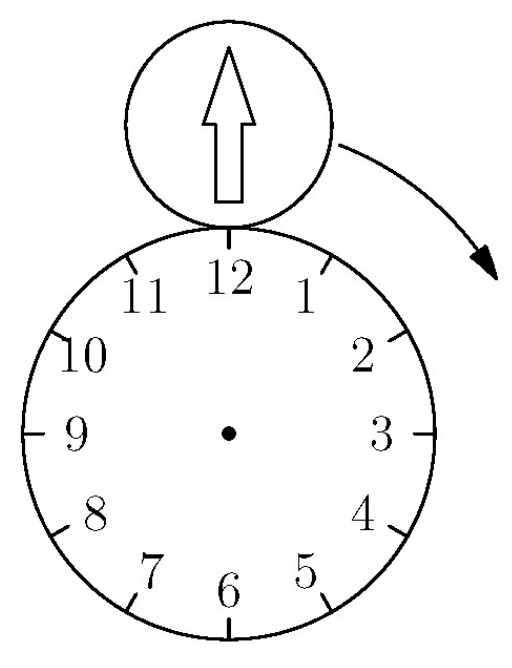
Answer Choices:
A. o'clock
B. o'clock
C. o'clock
D. o'clock
E. o'clock
Solution:
Problem 15: Consider the set of all fractions , where and are relatively prime positive integers. How many of these fractions have the property that if both numerator and denominator are increased by , the value of the fraction is increased by ?
Answer Choices:
A.
B.
C.
D.
E. infinitely many
Solution:
Problem 16: If , , and , what is the value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: A line that passes through the origin intersects both the line and the line . The three lines create an equilateral triangle. What is the perimeter of the triangle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: Hexadecimal (base-) numbers are written using the numeric digits through as well as the letters through to represent through . Among the first positive integers, there are whose hexadecimal representation contains only numeric digits. What is the sum of the digits of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: The isosceles right triangle has right angle at and area . The rays trisecting intersect at and . What is the area of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: A rectangle has area and perimeter , where and are positive integers. Which of the following numbers cannot equal ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Tetrahedron has , and . What is the volume of the tetrahedron?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Eight people are sitting around a circular table, each holding a fair coin. All eight people flip their coins and those who flip heads stand while those who flip tails remain seated. What is the probability that no two adjacent people will stand?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: The zeros of the function are integers. What is the sum of the possible values of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: For some positive integers , quadrilateral with positive integer side lengths has perimeter , right angles at and , , and . How many different values of are possible?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Let be a square of side length . Two points are chosen independently at random on the sides of . The probability that the straight-line distance between the points is at least is , where , and are positive integers and . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions