¶ 2014 AMC 10B Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2014 AMC 10B problems here.
Discussion Forum
Engage in discussion about the 2014 AMC 10B math contest by visiting Random Math AMC 10B 2014 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2014 AMC 10B problems, please refer below:
Problem 1: Leah has coins, all of which are pennies and nickels. If she had one more nickel than she has now, then she would have the same number of pennies and nickels. In cents, how much are Leah's coins worth?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: Randy drove the first third of his trip on a gravel road, the next miles on pavement, and the remaining one-fifth on a dirt road. In miles, how long was Randy's trip?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Susie pays for muffins and bananas. Calvin spends twice as much paying for muffins and bananas. A muffin is how many times as expensive as a banana?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Doug constructs a square window using equal-size panes of glass, as shown. The ratio of the height to width for each pane is , and the borders around and between the panes are inches wide. In inches, what is the side length of the square window?

Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: Orvin went to the store with just enough money to buy balloons. When he arrived he discovered that the store had a special sale on balloons: buy balloon at the regular price and get a second at off the regular price. What is the greatest number of balloons Orvin could buy?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: Suppose and is greater than . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: A truck travels feet every seconds. There are feet in a yard. How many yards does the truck travel in minutes?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: For real numbers and ,
What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: In the addition shown below , and are distinct digits. How many different values are possible for ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: For the consumer, a single discount of is more advantageous than any of the following discounts:
() two successive discounts.
() three successive discounts.
() a discount followed by a discount.
What is the smallest possible positive integer value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: The largest divisor of is itself. What is its fifth largest divisor?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
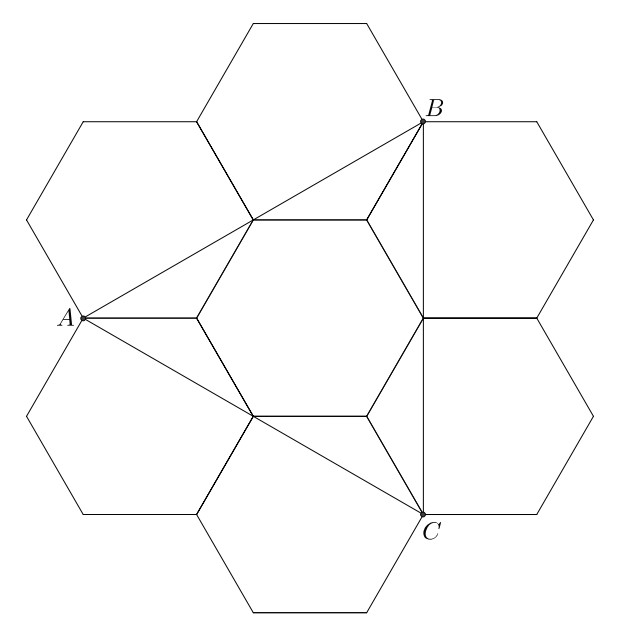
Problem 13: Six regular hexagons surround a regular hexagon of side length as shown. What is the area of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Danica drove her new car on a trip for a whole number of hours, averaging miles per hour. At the beginning of the trip, miles was displayed on the odometer, where is a -digit number with and . At the end of the trip, the odometer showed miles. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
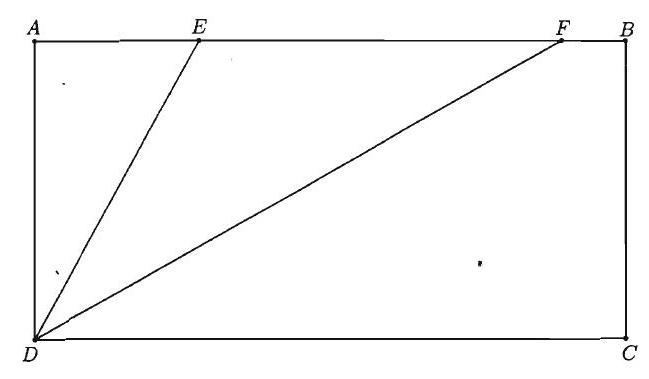
Problem 15: In rectangle and points and lie on so that and trisect as shown. What is the ratio of the area of to the area of rectangle ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: Four fair six-sided dice are rolled. What is the probability that at least three of the four dice show the same value?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: What is the greatest power of that is a factor of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: A list of positive integers has a mean of , a median of , and a unique mode of . What is the largest possible value of an integer in the list?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: Two concentric circles have radii and . Two points on the outer circle are chosen independently and uniformly at random. What is the probability that the chord joining the two points intersects the inner circle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: For how many integers is the number negative?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Trapezoid has parallel sides of length and of length . The other two sides are of lengths and . The angles at and are acute. What is the length of the shorter diagonal of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
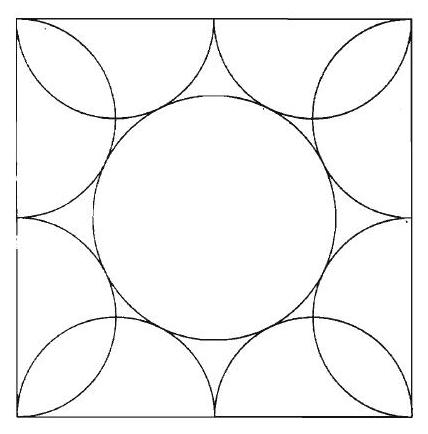
Problem 22: Eight semicircles line the inside of a square with side length as shown. What is the radius of the circle tangent to all of these semicircles?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: A sphere is inscribed in a truncated right circular cone as shown. The volume of the truncated cone is twice that of the sphere. What is the ratio of the radius of the bottom base of the truncated cone to the radius of the top base of the truncated cone?
.jpg)
Answer Choices:
A.
B.
C. \sqrt
D.
E.
Solution:
Problem 24: The numbers are to be arranged in a circle. An arrangement is bad if it is not true that for every from to one can find a subset of the numbers that appear consecutively on the circle that sum to . Arrangements that differ only by a rotation or a reflection are considered the same. How many different bad arrangements are there?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: In a small pond there are eleven lily pads in a row labeled through . A frog is sitting on pad . When the frog is on pad , it will jump to pad with probability and to pad with probability . Each jump is independent of the previous jumps. If the frog reaches pad it will be eaten by a patiently waiting snake. If the frog reaches pad it will exit the pond, never to return. What is the probability that the frog will escape being eaten by the snake?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions