¶ 2006 AMC 12B Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2006 AMC 12B problems here.
Discussion Forum
Engage in discussion about the 2006 AMC 12B math contest by visiting Random Math AMC 12B 2006 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2006 AMC 12B problems, please refer below:
Problem 1: What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: For real numbers and , define . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: A football game was played between two teams, the Cougars and the Panthers. The two teams scored a total of points, and the Cougars won by a margin of points. How many points did the Panthers score?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Mary is about to pay for five items at the grocery store. The prices of the items are , and . Mary will pay with a twenty-dollar bill. Which of the following is closest to the percentage of the that she will receive in change?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: John is walking east at a speed of miles per hour, while Bob is also walking east, but at a speed of miles per hour. If Bob is now mile west of John, how many minutes will it take for Bob to catch up to John?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: Francesca uses grams of lemon juice, grams of sugar, and grams of water to make lemonade. There are calories in grams of lemon juice and calories in grams of sugar. Water contains no calories. How many calories are in grams of her lemonade?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: Mr. and Mrs. Lopez have two children. When they get into their family car, two people sit in the front, and the other two sit in the back. Either Mr. Lopez or Mrs. Lopez must sit in the driver's seat. How many seating arrangements are possible?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: The lines and intersect at the point . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: How many even three-digit integers have the property that their digits, read left to right, are in strictly increasing order?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: In a triangle with integer side lengths, one side is three times as long as a second side, and the length of the third side is . What is the greatest possible perimeter of the triangle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: Joe and JoAnn each bought ounces of coffee in a -ounce cup. Joe drank ounces of his coffee and then added ounces of cream. JoAnn added ounces of cream, stirred the coffee well, and then drank ounces. What is the resulting ratio of the amount of cream in Joe's coffee to that in JoAnn's coffee?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: The parabola has vertex and -intercept , where . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Rhombus is similar to rhombus . The area of rhombus is , and . What is the area of rhombus ?
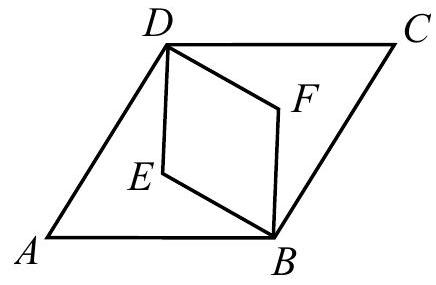
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Elmo makes sandwiches for a fundraiser. For each sandwich he uses globs of peanut butter at cents per glob and blobs of jam at cents per blob. The cost of the peanut butter and jam to make all the sandwiches is . Assume that , , and are positive integers with . What is the cost of the jam Elmo uses to make the sandwiches?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: Circles with centers and have radii and , respectively, and are externally tangent. Points and are on the circle centered at , and points and are on the circle centered at , such that and are common external tangents to the circles. What is the area of hexagon ?
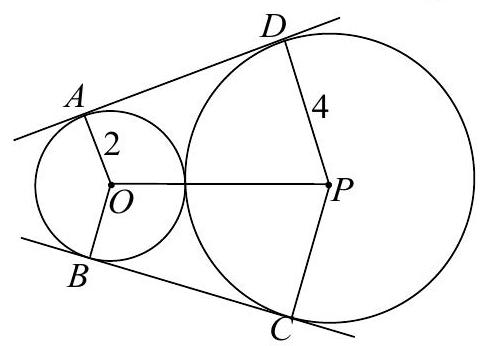
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: Regular hexagon has vertices and at and , respectively. What is its area?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: For a particular peculiar pair of dice, the probabilities of rolling , and on each die are in the ratio . What is the probability of rolling a total of on the two dice?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: An object in the plane moves from one lattice point to another. At each step, the object may move one unit to the right, one unit to the left, one unit up, or one unit down. If the object starts at the origin and takes a ten-step path, how many different points could be the final point?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: Mr. Jones has eight children of different ages. On a family trip his oldest child, who is , spots a license plate with a -digit number in which each of two digits appears two times. "Look, daddy!" she exclaims. "That number is evenly divisible by the age of each of us kids!" "That's right," replies Mr. Jones, "and the last two digits just happen to be my age." Which of the following is the age of one of Mr. Jones's children?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Let be chosen at random from the interval . What is the probability that
Here denotes the greatest integer that is less than or equal to .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Rectangle has area . An ellipse with area passes through and and has foci at and . What is the perimeter of the rectangle? (The area of an ellipse is , where and are the lengths of its axes.)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Suppose , and are positive integers with , and , where and are integers and is not divisible by . What is the smallest possible value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: Isosceles has a right angle at . Point is inside , such that , and . Legs and have length , where and are positive integers. What is ?
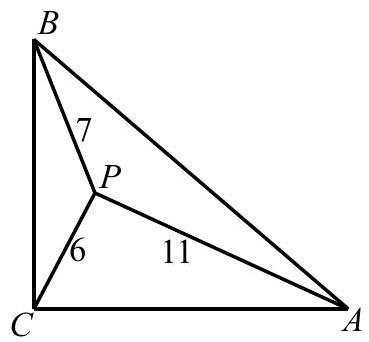
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Let be the set of all points in the coordinate plane such that and . What is the area of the subset of for which
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: A sequence of non-negative integers is defined by the rule for . If , and , how many different values of are possible?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions