¶ 2006 AMC 12A Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2006 AMC 12A problems here.
Discussion Forum
Engage in discussion about the 2006 AMC 12A math contest by visiting Random Math AMC 12A 2006 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2006 AMC 12A problems, please refer below:
Problem 1: Sandwiches at Joe's Fast Food cost each and sodas cost each. How many dollars will it cost to purchase sandwiches and sodas?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: Define . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: The ratio of Mary's age to Alice's age is . Alice is years old. How old is Mary?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: A digital watch displays hours and minutes with AM and PM. What is the largest possible sum of the digits in the display?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Doug and Dave shared a pizza with equally-sized slices. Doug wanted a plain pizza, but Dave wanted anchovies on half of the pizza. The cost of a plain pizza was , and there was an additional cost of for putting anchovies on one half. Dave ate all the slices of anchovy pizza and one plain slice. Doug ate the remainder. Each then paid for what he had eaten. How many more dollars did Dave pay than Doug?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: The rectangle is cut into two congruent hexagons, as shown, in such a way that the two hexagons can be repositioned without overlap to form a square. What is ?
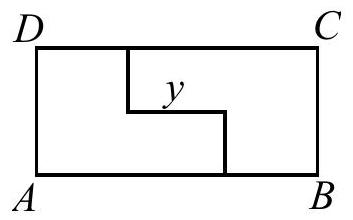
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: Mary is older than Sally, and Sally is younger than Danielle. The sum of their ages is years. How old will Mary be on her next birthday?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: How many sets of two or more consecutive positive integers have a sum of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: Oscar buys pencils and 3 erasers for . A pencil costs more than an eraser, and both items cost a whole number of cents. What is the total cost, in cents, of one pencil and one eraser?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: For how many real values of is an integer?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: Which of the following describes the graph of the equation ?
Answer Choices:
A. the empty set
B. one point
C. two lines
D. a circle
E. the entire plane
Solution:
Problem 12: A number of linked rings, each thick, are hanging on a peg. The top ring has an outside diameter of . The outside diameter of each of the other rings is less than that of the ring above it. The bottom ring has an outside diameter of . What is the distance, in , from the top of the top ring to the bottom of the bottom ring?
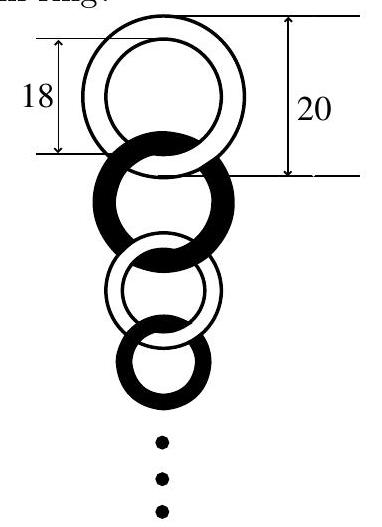
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: The vertices of a right triangle are the centers of three mutually externally tangent circles, as shown. What is the sum of the areas of these circles?
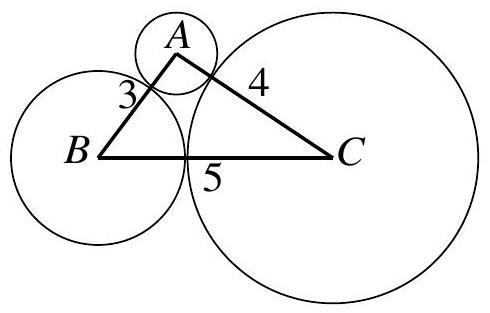
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Two farmers agree that pigs are worth and that goats are worth . When one farmer owes the other money, he pays the debt in pigs or goats, with "change" received in the form of goats or pigs as necessary. (For example, a debt could be paid with two pigs, with one goat received in change.) What is the amount of the smallest positive debt that can be resolved in this way?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: Suppose and . What is the smallest possible positive value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: Circles with centers and have radii and , respectively. A common internal tangent intersects the circles at and , respectively. Lines and intersect at , and . What is ?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Square has side length , a circle centered at has radius , and and are both rational. The circle passes through , and lies on . Point lies on the circle, on the same side of as . Segment is tangent to the circle, and . What is ?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: The function has the property that for each real number in its domain, is also in its domain and
What is the largest set of real numbers that can be in the domain of ?
Answer Choices:
A.
B.
C.
D. and and
E.
Solution:
Problem 19: Circles with centers and have radii and , respectively. The equation of a common external tangent to the circles can be written in the form with . What is ?
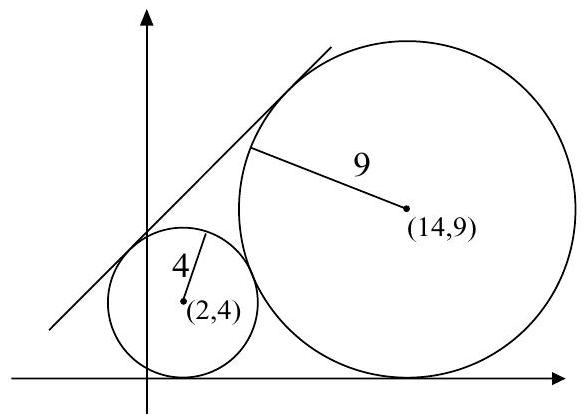
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: A bug starts at one vertex of a cube and moves along the edges of the cube according to the following rule. At each vertex the bug will choose to travel along one of the three edges emanating from that vertex. Each edge has equal probability of being chosen, and all choices are independent. What is the probability that after seven moves the bug will have visited every vertex exactly once?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Let
and
What is the ratio of the area of to the area of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: A circle of radius is concentric with and outside a regular hexagon of side length . The probability that three entire sides of the hexagon are visible from a randomly chosen point on the circle is . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: Given a finite sequence of real numbers, let be the sequence
of real numbers. Define and, for each integer 1 , define . Suppose , and let . If , then what is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: The expression
is simplified by expanding it and combining like terms. How many terms are in the simplified expression?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: How many non-empty subsets of have the following two properties?
(1) No two consecutive integers belong to .
(2) If contains elements, then contains no number less than .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions