¶ 2007 AMC 12B Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2007 AMC 12B problems here.
Discussion Forum
Engage in discussion about the 2007 AMC 12B math contest by visiting Random Math AMC 12B 2007 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2007 AMC 12B problems, please refer below:
Problem 1: Isabella's house has bedrooms. Each bedroom is feet long, feet wide, and feet high. Isabella must paint the walls of all the bedrooms. Doorways and windows, which will not be painted, occupy square feet in each bedroom. How many square feet of walls must be painted?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: A college student drove his compact car miles home for the weekend and averaged miles per gallon. On the return trip the student drove his parents' SUV and averaged only miles per gallon. What was the average gas mileage, in miles per gallon, for the round trip?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: The point is the center of the circle circumscribed about , with and , as shown. What is the degree measure of ?
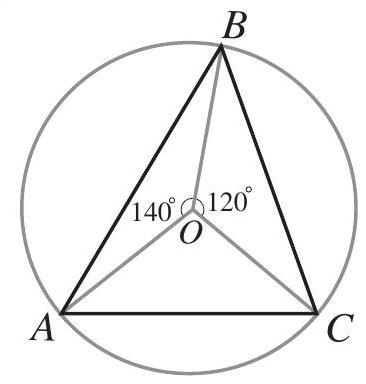
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: At Frank's Fruit Market, bananas cost as much as apples, and apples cost as much as oranges. How many oranges cost as much as bananas?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: The AMC contests will be scored by awarding points for each correct response, points for each incorrect response, and points for each problem left unanswered. After looking over the problems, Sarah has decided to attempt the first and leave the last unanswered. How many of the first problems must she solve correctly in order to score at least points?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: Triangle has side lengths , and . Two bugs start simultaneously from and crawl along the sides of the triangle in opposite directions at the same speed. They meet at point . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: All sides of the convex pentagon are of equal length, and . What is the degree measure of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Tom's age is years, which is also the sum of the ages of his three children. His age years ago was twice the sum of their ages then. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: A function has the property that for all real numbers . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Some boys and girls are having a car wash to raise money for a class trip to China. Initially of the group are girls. Shortly thereafter two girls leave and two boys arrive, and then of the group are girls. How many girls were initially in the group?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: The angles of quadrilateral satisfy . What is the degree measure of , rounded to the nearest whole number?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: A teacher gave a test to a class in which of the students are juniors and are seniors. The average score on the test was . The juniors all received the same score, and the average score of the seniors was . What score did each of the juniors receive on the test?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: A traffic light runs repeatedly through the following cycle: green for 30 seconds, then yellow for seconds, and then red for seconds. Leah picks a random three-second time interval to watch the light. What is the probability that the color changes while she is watching?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Point is inside equilateral . Points , and are the feet of the perpendiculars from to , and , respectively. Given that , , and , what is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: The geometric series has a sum of , and the terms involving odd powers of have a sum of . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: Each face of a regular tetrahedron is painted either red, white, or blue. Two colorings are considered indistinguishable if two congruent tetrahedra with those colorings can be rotated so that their appearances are identical. How many distinguishable colorings are possible?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: If is a nonzero integer and is a positive number such that , what is the median of the set ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: Let , and be digits with . The three-digit integer lies one third of the way from the square of a positive integer to the square of the next larger integer. The integer lies two thirds of the way between the same two squares. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: Rhombus , with side length , is rolled to form a cylinder of volume by taping to . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: The parallelogram bounded by the lines , and has area . The parallelogram bounded by the lines , , and has area . Given that , and are positive integers, what is the smallest possible value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: The first positive integers are each written in base . How many of these base- representations are palindromes? (A palindrome is a number that reads the same forward and backward.)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Two particles move along the edges of equilateral in the direction
starting simultaneously and moving at the same speed. One starts at , and the other starts at the midpoint of . The midpoint of the line segment joining the two particles traces out a path that encloses a region . What is the ratio of the area of to the area of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: How many non-congruent right triangles with positive integer leg lengths have areas that are numerically equal to times their perimeters?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: How many pairs of positive integers are there such that and
is an integer?
Answer Choices:
A.
B.
C.
D.
E. infinitely many
Solution:
Problem 25: Points , and are located in -dimensional space with and . The plane of is parallel to . What is the area of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions