¶ 2008 AMC 12A Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2008 AMC 12A problems here.
Discussion Forum
Engage in discussion about the 2008 AMC 12A math contest by visiting Random Math AMC 12A 2008 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2008 AMC 12A problems, please refer below:
Problem 1: A bakery owner turns on his doughnut machine at 8:30 Am. At 11:10 AM the machine has completed one third of the day's job. At what time will the doughnut machine complete the job?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: What is the reciprocal of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: Suppose that of bananas are worth as much as oranges. How many oranges are worth as much as of bananas?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Which of the following is equal to the product
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Suppose that
is an integer. Which of the following statements must be true about ?
Answer Choices:
A. It is negative.
B. It is even, but not necessarily a multiple of .
C. It is a multiple of , but not necessarily even.
D. It is a multiple of , but not necessarily a multiple of .
E. It is a multiple of .
Solution:
Problem 6: Heather compares the price of a new computer at two different stores. Store A offers off the sticker price followed by a rebate, and store B offers off the same sticker price with no rebate. Heather saves by buying the computer at store A instead of store B. What is the sticker price of the computer, in dollars?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: While Steve and LeRoy are fishing mile from shore, their boat springs a leak, and water comes in at a constant rate of gallons per minute. The boat will sink if it takes in more than gallons of water. Steve starts rowing toward the shore at a constant rate of miles per hour while LeRoy bails water out of the
boat. What is the slowest rate, in gallons per minute, at which LeRoy can bail if they are to reach the shore without sinking?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: What is the volume of a cube whose surface area is twice that of a cube with volume ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: Older television screens have an aspect ratio of . That is, the ratio of the width to the height is . The aspect ratio of many movies is not , so they are sometimes shown on a television screen by "letterboxing" — darkening strips of equal height at the top and bottom of the screen, as shown. Suppose a movie has an aspect ratio of and is shown on an older television screen with a -inch diagonal. What is the height, in inches, of each darkened strip?

Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Doug can paint a room in hours. Dave can paint the same room in hours. Doug and Dave paint the room together and take a one-hour break for lunch. Let be the total time, in hours, required for them to complete the job working together, including lunch. Which of the following equations is satisfied by ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: Three cubes are each formed from the pattern shown. They are then stacked on a table one on top of another so that the visible numbers have the greatest possible sum. What is that sum?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: A function has domain and range . (The notation denotes .) What are the domain and range, respectively, of the function defined by ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Points and lie on a circle centered at , and . A second circle is internally tangent to the first and tangent to both and . What is the ratio of the area of the smaller circle to that of the larger circle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: What is the area of the region defined by the inequality ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: Let . What is the units digit of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: The numbers , and are the first three terms of an arithmetic sequence, and the term of the sequence is . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Let be a sequence of integers determined by the rule if is even and if is odd. For how many positive integers is it true that is less than each of , and ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: Triangle , with sides of length , and , has one vertex on the positive -axis, one on the positive -axis, and one on the positive -axis. Let be the origin. What is the volume of tetrahedron ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: In the expansion of
what is the coefficient of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Triangle has , and . Point is on , and bisects the right angle. The inscribed circles of and have radii and , respectively. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: A permutation of is heavy-tailed if . What is the number of heavy-tailed permutations?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
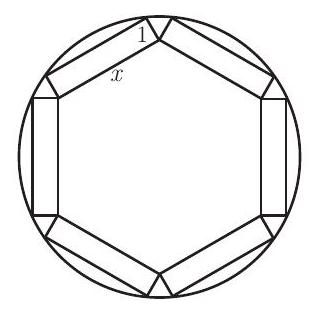
Problem 22: A round table has radius . Six rectangular place mats are placed on the table. Each place mat has width and length as shown. They are positioned so that each mat has two corners on the edge of the table, these two corners being end points of the same side of length . Further, the mats are positioned so that the inner corners each touch an inner corner of an adjacent mat. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: The solutions of the equation are the vertices of a convex polygon in the complex plane. What is the area of the polygon?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Triangle has and . Point is the midpoint of . What is the largest possible value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: A sequence of points in the coordinate plane satisfies
Suppose that . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions