¶ 2008 AMC 12B Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2008 AMC 12B problems here.
Discussion Forum
Engage in discussion about the 2008 AMC 12B math contest by visiting Random Math AMC 12B 2008 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2008 AMC 12B problems, please refer below:
Problem 1: A basketball player made baskets during a game. Each basket was worth either or points. How many different numbers could represent the total points scored by the player?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: A block of calendar dates is shown. The order of the numbers in the second row is to be reversed. Then the order of the numbers in the fourth row is to be reversed. Finally, the numbers on each diagonal are to be added. What will be the positive difference between the two diagonal sums?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: A semipro baseball league has teams with players each. League rules state that a player must be paid at least , and that the total of all players' salaries for each team cannot exceed . What is the maximum possible salary, in dollars, for a single player?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
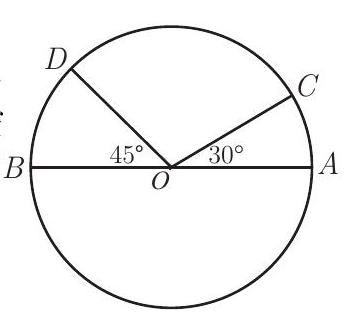
Problem 4: On circle , points and are on the same side of diameter , and . What is the ratio of the area of the smaller sector to the area of the circle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: A class collects to buy flowers for a classmate who is in the hospital. Roses cost each, and carnations cost each. No other flowers are to be used. How many different bouquets could be purchased for exactly ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: Postman Pete has a pedometer to count his steps. The pedometer records up to steps, then flips over to on the next step. Pete plans to determine his mileage for a year. On January Pete sets the pedometer to . During the year, the pedometer flips from to forty-four times. On December the pedometer reads . Pete takes steps per mile. Which of the following is closest to the number of miles Pete walked during the year?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: For real numbers and , define . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Points and lie on . The length of is times the length of , and the length of is times the length of . The length of is what fraction of the length of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: Points and are on a circle of radius and . Point is the midpoint of the minor arc . What is the length of the line segment ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Bricklayer Brenda would take hours to build a chimney alone, and bricklayer Brandon would take hours to build it alone. When they work together, they talk a lot, and their combined output is decreased by bricks per hour. Working together, they build the chimney in hours. How many bricks are in the chimney?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: A cone-shaped mountain has its base on the ocean floor and has a height of feet. The top of the volume of the mountain is above water. What is the depth of the ocean at the base of the mountain, in feet?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: For each positive integer , the mean of the first terms of a sequence is . What is the th term of the sequence?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Vertex of equilateral is in the interior of unit square . Let be the region consisting of all points inside and outside whose distance from is between and . What is the area of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: A circle has a radius of and a circumference of . What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: On each side of a unit square, an equilateral triangle of side length is constructed. On each new side of each equilateral triangle, another equilateral triangle of side length is constructed. The interiors of the square and the triangles have no points in common. Let be the region formed by the union of the square and all the triangles, and let be the smallest convex polygon that contains . What is the area of the region that is inside but outside ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: A rectangular floor measures feet by feet, where and are positive integers with . An artist paints a rectangle on the floor with the sides of the rectangle parallel to the sides of the floor. The unpainted part of the floor forms a border of width 1 foot around the painted rectangle and occupies half the area of the entire floor. How many possibilities are there for the ordered pair ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Let and be three distinct points on the graph of such that line is parallel to the -axis and is a right triangle with area . What is the sum of the digits of the -coordinate of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: A pyramid has a square base and vertex . The area of square is , and the areas of and are and , respectively. What is the volume of the pyramid?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: A function is defined by for all complex numbers , where and are complex numbers and . Suppose that and are both real. What is the smallest possible value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Michael walks at the rate of feet per second on a long straight path. Trash pails are located every feet along the path. A garbage truck travels at feet per second in the same direction as Michael and stops for seconds at each pail. As Michael passes a pail, he notices the truck ahead of him just leaving the next pail. How many times will Michael and the truck meet?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Two circles of radius 1 are to be constructed as follows. The center of circle is chosen uniformly and at random from the line segment joining to . The center of circle is chosen uniformly and at random, and independently of the first choice, from the line segment joining to . What is the probability that circles and intersect?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: A parking lot has spaces in a row. Twelve cars arrive, each of which requires one parking space, and their drivers choose their spaces at random from among the available spaces. Auntie Em then arrives in her SUV, which requires adjacent spaces. What is the probability that she is able to park?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: The sum of the base- logarithms of the divisors of is . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Let . Distinct points lie on the -axis, and distinct points lie on the graph of . For every positive integer is an equilateral triangle. What is the least for which the length ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Let be a trapezoid with , and . Bisectors of and meet at , and bisectors of and meet at . What is the area of hexagon ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions