¶ 2009 AMC 12A Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2009 AMC 12A problems here.
Discussion Forum
Engage in discussion about the 2009 AMC 12A math contest by visiting Random Math AMC 12A 2009 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2009 AMC 12A problems, please refer below:
Problem 1: Kim's flight took off from Newark at AM and landed in Miami at PM. Both cites are in the same time zone. If her flight took hours and minutes, with , what is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: Which of the following is equal to ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: What number is one third of the way from to ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Four coins are picked out of a piggy bank that contains a collection of pennies, nickels, dimes, and quarters. Which of the following could not be the total value of the four coins, in cents?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: One dimension of a cube is increased by , another is decreased by , and the third is left unchanged. The volume of the new rectangular solid is less than that of the cube. What was the volume of the cube?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: Suppose that and . Which of the following is equal to for every pair of integers ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: The first three terms of an arithmetic sequence are , and respectively. The th term of the sequence is . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Four congruent rectangles are placed as shown. The area of the outer square is times that of the inner square. What is the ratio of the length of the longer side of each rectangle to the length of its shorter side?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: Suppose that and . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: In quadrilateral , and is an integer. What is ?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: The figures and shown are the first in a sequence of figures. For is constructed from by surrounding it with a square and placing one more diamond on each side of the new square than had on each side of its outside square. For example, figure has diamonds. How many diamonds are there in figure ?
.jpg)
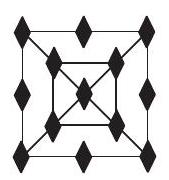
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: How many positive integers less than are times the sum of their digits?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: A ship sails miles in a straight line from to , turns through an angle between and , and then sails another miles to . Let be measured in miles. Which of the following intervals contains ?
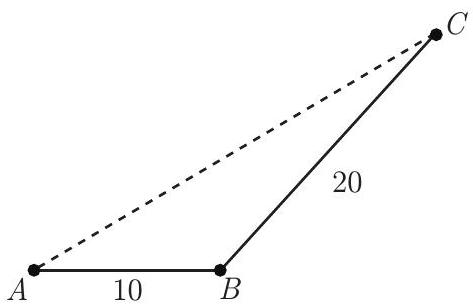
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: A triangle has vertices , and , and the line divides the triangle into two triangles of equal area. What is the sum of all possible values of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: For what value of is ? Note: here .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: A circle with center is tangent to the positive - and -axes and externally tangent to the circle centered at with radius . What is the sum of all possible radii of the circle with center ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Let and be two different infinite geometric series of positive numbers with the same first term. The sum of the first series is , and the sum of the second series is . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: For , let , where there are zeros between the and the . Let be the number of factors of in the prime factorization of . What is the maximum value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: Andrea inscribed a circle inside a regular pentagon, circumscribed a circle around the pentagon, and calculated the area of the region between the two circles. Bethany did the same with a regular heptagon ( sides). The areas of the two regions were and , respectively. Each polygon had a side length of . Which of the following is true?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Convex quadrilateral has and . Diagonals and intersect at , and and have equal areas. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Let , where , and are complex numbers. Suppose that
What is the number of nonreal zeros of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: A regular octahedron has side length . A plane parallel to two of its opposite faces cuts the octahedron into two congruent solids. The polygon formed by the intersection of the plane and the octahedron has area , where , and are positive integers, and are relatively prime, and is not divisible by the square of any prime. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: Functions and are quadratic, , and the graph of contains the vertex of the graph of . The four -intercepts on the two graphs have -coordinates , and , in increasing order, and . The value of is , where , and are positive integers, and is not divisible by the square of any prime. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: The tower function of twos is defined recursively as follows: and for . Let and . What is the largest integer such that
is defined?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: The first two terms of a sequence are and . For ,
What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions