¶ 2009 AMC 12B Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2009 AMC 12B problems here.
Discussion Forum
Engage in discussion about the 2009 AMC 12B math contest by visiting Random Math AMC 12B 2009 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2009 AMC 12B problems, please refer below:
Problem 1: Each morning of her five-day workweek, Jane bought either a -cent muffin or a -cent bagel. Her total cost for the week was a whole number of dollars. How many bagels did she buy?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: Paula the painter had just enough paint for identically sized rooms. Unfortunately, on the way to work, three cans of paint fell off her truck, so she had only enough paint for rooms. How many cans of paint did she use for the rooms?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: Twenty percent less than is one-third more than what number?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: A rectangular yard contains two flower beds in the shape of congruent isosceles right triangles. The remainder of the yard has a trapezoidal shape, as shown. The parallel sides of the trapezoid have lengths and meters. What fraction of the yard is occupied by the flower beds?

Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Kiana has two older twin brothers. The product of their three ages is . What is the sum of their three ages?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: By inserting parentheses, it is possible to give the expression
several values. How many different values can be obtained?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: In a certain year the price of gasoline rose by during January, fell by during February, rose by during March, and fell by during April. The price of gasoline at the end of April was the same as it had been at the beginning of January. To the nearest integer, what is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: When a bucket is two-thirds full of water, the bucket and water weigh kilograms. When the bucket is one-half full of water the total weight is kilograms. In terms of and , what is the total weight in kilograms when the bucket is full of water?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: Triangle has vertices , and , where is on the line . What is the area of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: A particular -hour digital clock displays the hour and minute of a day. Unfortunately, whenever it is supposed to display a , it mistakenly displays a . For example, when it is PM the clock incorrectly shows PM. What fraction of the day will the clock show the correct time?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: On Monday, Millie puts a quart of seeds, of which are millet, into a bird feeder. On each successive day she adds another quart of the same mix of seeds without removing any seeds that are left. Each day the birds eat only of the millet in the feeder, but they eat all of the other seeds. On which day, just after Millie has placed the seeds, will the birds find that more than half the seeds in the feeder are millet?
Answer Choices:
A. Tuesday
B. Wednesday
C. Thursday
D. Friday
E. Saturday
Solution:
Problem 12: The fifth and eighth terms of a geometric sequence of real numbers are and respectively. What is the first term?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Triangle has and , and the altitude to has length . What is the sum of the two possible values of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Five unit squares are arranged in the coordinate plane as shown, with the lower left corner at the origin. The slanted line, extending from to , divides the entire region into two regions of equal area. What is ?
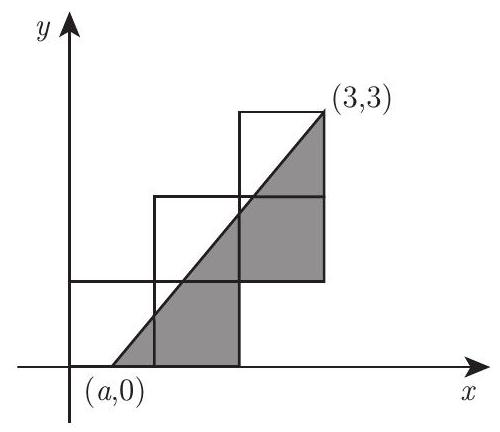
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: Assume . Below are five equations for . Which equation has the largest solution ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: Trapezoid has , and . The ratio is . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Each face of a cube is given a single narrow stripe painted from the center of one edge to the center of its opposite edge. The choice of the edge pairing is made at random and independently for each face. What is the probability that there is a continuous stripe encircling the cube?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: Rachel and Robert run on a circular track. Rachel runs counterclockwise and completes a lap every seconds, and Robert runs clockwise and completes a lap every seconds. Both start from the start line at the same time. At some random time between minutes and minutes after they begin to run, a photographer standing inside the track takes a picture that shows one-fourth of the track, centered on the starting line. What is the probability that both Rachel and Robert are in the picture?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: For each positive integer , let . What is the sum of all values of that are prime numbers?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: A convex polyhedron has vertices , and 100 edges. The polyhedron is cut by planes in such a way that plane cuts only those edges that meet at vertex . In addition, no two planes intersect inside or on . The cuts produce pyramids and a new polyhedron . How many edges does have?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Ten women sit in seats in a line. All of the get up and then reseat themselves using all seats, each sitting in the seat she was in before or a seat next to the one she occupied before. In how many ways can the women be reseated?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Parallelogram has area . Vertex is at and all other vertices are in the first quadrant. Vertices and are lattice points on the lines and for some integer , respectively. How many such parallelograms are there?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: A region in the complex plane is defined by
A complex number is chosen uniformly at random from . What is the probability that is also in ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: For how many values of in is ?
Note: The functions and denote inverse trigonometric functions.
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: The set is defined by the points with integer coordinates, , and . How many squares of side at least have their four vertices in ?
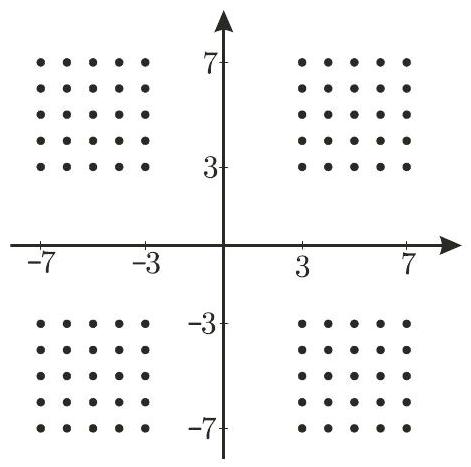
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions