¶ 2010 AMC 12A Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2010 AMC 12A problems here.
Discussion Forum
Engage in discussion about the 2010 AMC 12A math contest by visiting Random Math AMC 12A 2010 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2010 AMC 12A problems, please refer below:
Problem 1: What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: A ferry boat shuttles tourists to an island every hour starting at AM until its last trip, which starts at PM. One day the boat captain notes that on the AM trip there were tourists on the ferry boat, and that on each successive trip, the number of tourists was fewer than on the previous trip. How many tourists did the ferry take to the island that day?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: Rectangle , pictured below, shares of its area with square . Square shares of its area with rectangle . What is ?
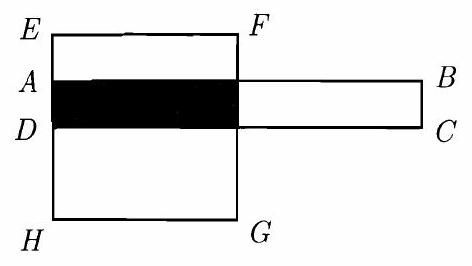
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: If , then which of the following must be positive?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Halfway through a -shot archery tournament, Chelsea leads by points. For each shot a bullseye scores points, with other possible scores being , and points. Chelsea always scores at least points on each shot. If Chelsea's next shots are bulleyes she will be guaranteed victory. What is the minimum value for ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: A palindrome, such as , is a number that remains the same when its digits are reversed. The numbers and are three-digit and four-digit palindromes, respectively. What is the sum of the digits of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: Logan is constructing a scaled model of his town. The city's water tower stands meters high, and the top portion is a sphere that holds liters of water. Logan's miniature water tower holds liters. How tall, in meters, should Logan make his tower?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Triangle has . Let and be on and , respectively, such that . Let be the intersection of segments and , and suppose that is equilateral. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: A solid cube has side length inches. A -inch by -inch square hole is cut into the center of each face. The edges of each cut are parallel to the edges of the cube, and each hole goes all the way through the cube. What is the volume, in cubic inches, of the remaining solid?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: The first four terms of an arithmetic sequence are , and . What is the term of this sequence?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: The solution of the equation can be expressed in the form . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: In a magical swamp there are two species of talking amphibians: toads, whose statements are always true, and frogs, whose statements are always false. Four amphibians, Brian, Chris, LeRoy, and Mike live together in this swamp, and they make the following statements.
Brian: "Mike and I are different species."
Chris: "LeRoy is a frog."
LeRoy: "Chris is a frog."
Mike: "Of the four of us, at least two are toads."
How many of these four amphibians are frogs?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: For how many integer values of do the graphs of and not intersect?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Nondegenerate has integer side lengths, is an angle bisector, 3 , and . What is the smallest possible value of the perimeter?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: A coin is altered so that the probability that it lands on heads is less than than and when the coin is flipped four times, the probability of an equal number of heads and tails is . What is the probability that the coin lands on heads?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: Bernardo randomly picks 3 distinct numbers from the set and arranges them in descending order to form a -digit number. Silvia randomly picks distinct numbers from the set and also arranges them in descending order to form a -digit number. What is the probability that Bernardo's number is larger than Silvia's number?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Equiangular hexagon has side lengths and . The area of is of the area of the hexagon. What is the sum of all possible values of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: A -step path is to go from to with each step increasing either the -coordinate or the -coordinate by . How many such paths stay outside or on the boundary of the square at each step?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: Each of boxes in a line contains a single red marble, and for , the box in the position also contains white marbles. Isabella begins at the first box and successively draws a single marble at random from each box, in order. She stops when she first draws a red marble. Let be the probability that Isabella stops after drawing exactly marbles. What is the smallest value of for which ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Arithmetic sequences and have integer terms with and for some . What is the largest possible value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: The graph of lies above the line except at three values of , where the graph and the line intersect. What is the largest of those values?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: What is the minimum value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: The number obtained from the last two nonzero digits of is equal to . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Let . The intersection of the domain of with the interval is a union of disjoint open intervals. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Two quadrilaterals are considered the same if one can be obtained from the other by a rotation and a translation. How many different convex cyclic quadrilaterals are there with integer sides and perimeter equal to ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions