¶ 2010 AMC 12B Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2010 AMC 12B problems here.
Discussion Forum
Engage in discussion about the 2010 AMC 12B math contest by visiting Random Math AMC 12B 2010 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2010 AMC 12B problems, please refer below:
Problem 1: Makayla attended two meetings during her -hour work day. The first meeting took minutes and the second meeting took twice as long. What percent of her work day was spent attending meetings?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: A big is formed as shown. What is its area?
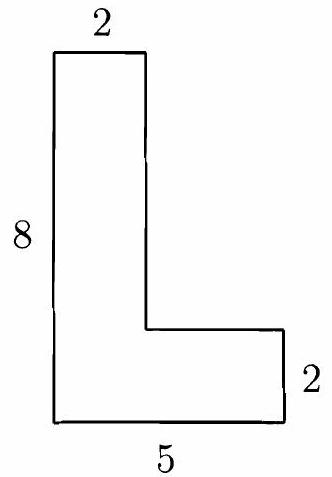
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: A ticket to a school play costs dollars, where is a whole number. A group of graders buys tickets costing a total of , and a group of graders buys tickets costing a total of . How many values for are possible?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: A month with days has the same number of Mondays and Wednesdays. How many of the seven days of the week could be the first day of this month?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Lucky Larry's teacher asked him to substitute numbers for , and in the expression and evaluate the result. Larry ignored the parentheses but added and subtracted correctly and obtained the correct result by coincidence. The numbers Larry substituted for , and were , and , respectively. What number did Larry substitute for ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: At the beginning of the school year, of all students in Mr. Wells' math class answered "Yes" to the question "Do you love math", and answered "No." At the end of the school year, answered "Yes" and answered "No." Altogether, of the students gave a different answer at the beginning and end of the school year. What is the difference between the maximum and the minimum possible values of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: Shelby drives her scooter at a speed of miles per hour if it is not raining, and miles per hour if it is raining. Today she drove in the sun in the morning and in the rain in the evening, for a total of miles in minutes. How many minutes did she drive in the rain?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Every high school in the city of Euclid sent a team of students to a math contest. Each participant in the contest received a different score. Andrea's score was the median among all students, and hers was the highest score on her team. Andrea's teammates Beth and Carla placed and , respectively. How many schools are in the city?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: Let be the smallest positive integer such that is divisible by is a perfect cube, and is a perfect square. What is the number of digits of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: The average of the numbers , and is . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: A palindrome between and is chosen at random. What is the probability that it is divisible by ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: For what value of does
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: In and . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Let , and be positive integers with , and let be the largest of the sums and . What is the smallest possible value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: For how many ordered triples of nonnegative integers less than are there exactly two distinct elements in the set , where ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: Positive integers , and are randomly and independently selected with replacement from the set . What is the probability that is divisible by ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: The entries in a array include all the digits from through , arranged so that the entries in every row and column are in increasing order. How many such arrays are there?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: A frog makes jumps, each exactly meter long. The directions of the jumps are chosen independently and at random. What is the probability that the frog's final position is no more than meter from its starting position?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: A high school basketball game between the Raiders and the Wildcats was tied at the end of the first quarter. The number of points scored by the Raiders in each of the four quarters formed an increasing geometric sequence, and the number of points scored by the Wildcats in each of the four quarters formed an increasing arithmetic sequence. At the end of the fourth quarter, the Raiders had won by one point. Neither team scored more than points. What was the total number of points scored by the two teams in the first half?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: A geometric sequence has , and for some real number . For what value of does ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Let , and let be a polynomial with integer coefficients such that
What is the smallest possible value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Let be a cyclic quadrilateral. The side lengths of are distinct integers less than such that . What is the largest possible value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: Monic quadratic polynomials and have the property that has zeros at , and , and has zeros at , and . What is the sum of the minimum values of and ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: The set of real numbers for which
is the union of intervals of the form . What is the sum of the lengths of these intervals?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: For every integer , let pow be the largest power of the largest prime that divides . For example pow . What is the largest integer such that divides
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions