¶ 2014 AMC 12B Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2014 AMC 12B problems here.
Discussion Forum
Engage in discussion about the 2014 AMC 12B math contest by visiting Random Math AMC 12B 2014 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2014 AMC 12B problems, please refer below:
Problem 1: Leah has coins, all of which are pennies and nickels. If she had one more nickel than she has now, then she would have the same number of pennies and nickels. In cents, how much are Leah's coins worth?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: Orvin went to the store with just enough money to buy balloons. When he arrived he discovered that the store had a special sale on balloons: buy balloon at the regular price and get a second at off the regular price. What is the greatest number of balloons Orvin could buy?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: Randy drove the first third of his trip on a gravel road, the next miles on pavement, and the remaining one-fifth on a dirt road. In miles, how long was Randy's trip?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Susie pays for muffins and bananas. Calvin spends twice as much paying for muffins and bananas. A muffin is how many times as expensive as a banana?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Doug constructs a square window using equal-size panes of glass, as shown. The ratio of the height to width for each pane is , and the borders around and between the panes are inches wide. In inches, what is the side length of the square window?

Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: Ed and Ann both have lemonade with their lunch. Ed orders the regular size. Ann gets the large lemonade, which is more than the regular. After both consume of their drinks, Ann gives Ed a third of what she has left, and additional ounces. When they finish their lemonades they realize that they both drank the same amount. How many ounces of lemonade did they drink together?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: For how many positive integers is also a positive integer?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: In the addition shown below , and are distinct digits. How many different values are possible for ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: Convex quadrilateral has , and , as shown. What is the area of the quadrilateral?
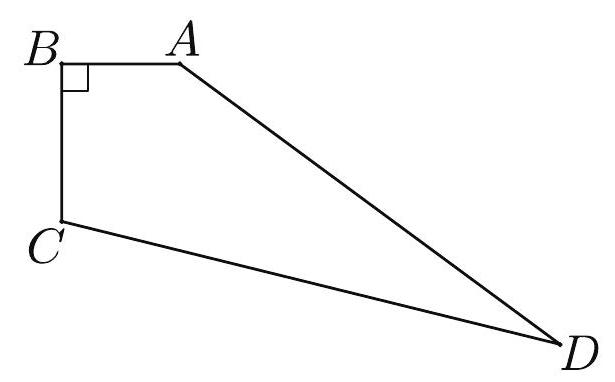
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Danica drove her new car on a trip for a whole number of hours, averaging 55 miles per hour. At the beginning of the trip, miles was displayed on the odometer, where is a 3 -digit number with and . At the end of the trip, the odometer showed miles. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: A list of positive integers has a mean of , a median of , and a unique mode of . What is the largest possible value of an integer in the list?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: A set consists of triangles whose sides have integer lengths less than , and no two elements of are congruent or similar. What is the largest number of elements that can have?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Real numbers and are chosen with such that no triangle with positive area has side lengths , and or , and . What is the smallest possible value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: A rectangular box has a total surface area of square inches. The sum of the lengths of all its edges is inches. What is the sum of the lengths in inches of all of its interior diagonals?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: When , the number is an integer. What is the largest power of that is a factor of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: Let be a cubic polynomial with , and . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Let be the parabola with equation and let . There are real numbers and such that the line through with slope does not intersect if and only if . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: The numbers are to be arranged in a circle. An arrangement is bad if it is not true that for every from to one can find a subset of the numbers that appear consecutively on the circle that sum to . Arrangements that differ only by a rotation or a reflection are considered the same. How many different bad arrangements are there?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: A sphere is inscribed in a truncated right circular cone as shown. The volume of the truncated cone is twice that of the sphere. What is the ratio of the radius of the bottom base of the truncated cone to the radius of the top base of the truncated cone?

Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: For how many positive integers is ?
Answer Choices:
A.
B.
C.
D.
E. infinitely many
Solution:
Problem 21: In the figure, is a square of side length . The rectangles and are congruent. What is ?
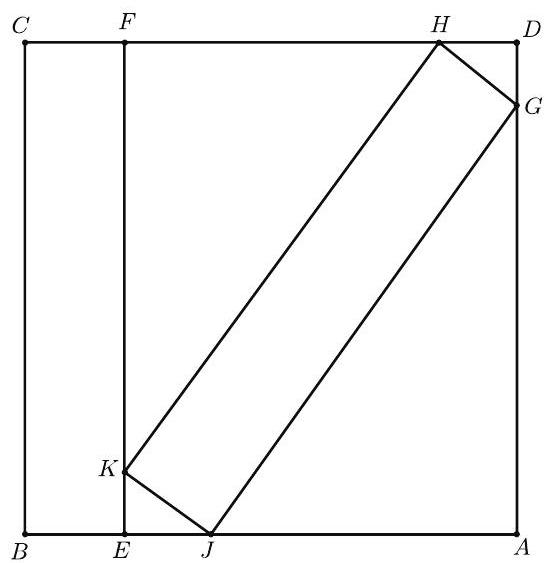
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: In a small pond there are eleven lily pads in a row labeled through . A frog is sitting on pad . When the frog is on pad , it will jump to pad with probability and to pad with probability . Each jump is independent of the previous jumps. If the frog reaches pad it will be eaten by a patiently waiting snake. If the frog reaches pad it will exit the pond, never to return. What is the probability that the frog will escape being eaten by the snake?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: The number is prime. Let . What is the remainder when is divided by ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Let be a pentagon inscribed in a circle such that , , and . The sum of the lengths of all diagonals of is equal to , where and are relatively prime positive integers. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: What is the sum of all positive real solutions to the equation
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions