¶ 2020 AMC 12B Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2020 AMC 12B problems here.
Discussion Forum
Engage in discussion about the 2020 AMC 12B math contest by visiting Random Math AMC 12B 2020 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2020 AMC 12B problems, please refer below:
Problem 1: What is the value in simplest form of the following expression?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: What is the value of the following expression?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: The ratio of to is , the ratio of to is , and the ratio of to is . What is the ratio of to ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: The acute angles of a right triangle are and , where and both and are prime numbers. What is the least possible value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Teams and are playing in a basketball league where each game results in a win for one team and a loss for the other team. Team has won of its games and team has won of its games. Also, team has won more games and lost more games than team . How many games has team played?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: For all integers , the value of
is always which of the following?
Answer Choices:
A. a multiple of
B. a multiple of
C. a prime number
D. a perfect square
E. a perfect cube
Solution:
Problem 7: Two nonhorizontal, non vertical lines in the -coordinate plane intersect to form a angle. One line has slope equal to times the slope of the other line. What is the greatest possible value of the product of the slopes of the two lines?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: How many ordered pairs of integers satisfy the equation
Answer Choices:
A.
B.
C.
D.
E. infinitely many
Solution:
Problem 9: A three-quarter sector of a circle of radius inches together with its interior can be rolled up to form the lateral surface area of a right circular cone by taping together along the two radii shown. What is the volume of the cone in cubic inches?
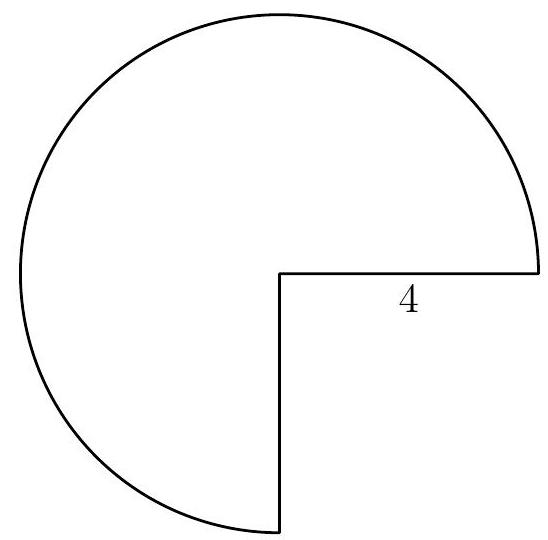
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: In unit square , the inscribed circle intersects at , and intersects at a point different from . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: As shown in the figure below, six semicircles lie in the interior of a regular hexagon with side length so that the diameters of the semicircles coincide with the sides of the hexagon. What is the area of the shaded regioninside the hexagon but outside all of the semicircles?
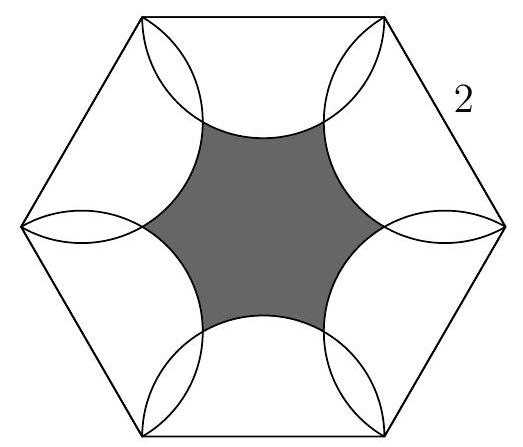
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: Let be a diameter in a circle of radius . Let be a chord in the circle that intersects at a point such that and . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Which of the following is the value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Bela and Jenn play the following game on the closed interval of the real number line, where is a fixed integer greater than . They take turns playing, with Bela going first. At his first turn, Bela chooses any real number in the interval . Thereafter, the player whose turn it is chooses a real number that is more than one unit away from all numbers previously chosen by either player. A player unable to choose such a number loses. Using optimal strategy, which player will win the game?
Answer Choices:
A. Bela will always win.
B. Jenn will always win.
C. Bela will win if and only if is odd.
D. Jenn will win
E. Jenn will win if and only if
Solution:
Problem 15: There are people standing equally spaced around a circle. Each person knows exactly of the other people: the people standing next to her or him, as well as the person directly across the circle. How many ways are there for the people to split up into pairs so that the members of each pair know each other?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: An urn contains one red ball and one blue ball. A box of extra red and blue balls lie nearby. George performs the following operation four times: he draws a ball from the urn at random and then takes a ball of the same color from the box and returns those two matching balls to the urn. After the four iterations the urn contains six balls. What is the probability that the urn contains three balls of each color?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: How many polynomials of the form , where , and are real numbers, have the property that whenever is a root, so is ? (Note that )
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: In square , points and lie on and , respectively, so that . Points and lie on and , respectively, and points and lie on so that and . See the figure below. Triangle , quadrilateral , quadrilateral , and pentagon each has area . What is ?
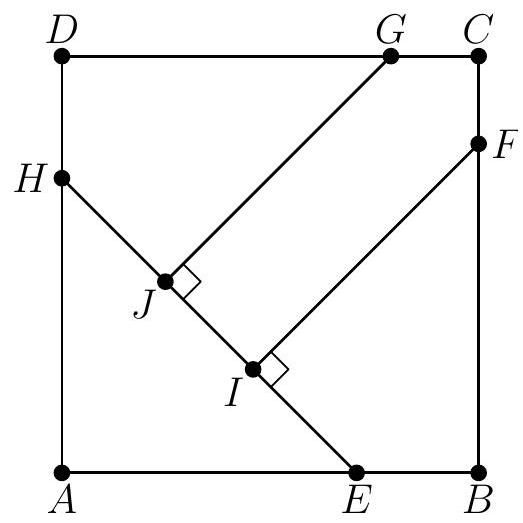
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: Square in the coordinate plane has vertices at the points , and . Consider the following four transformations:
-
, a rotation of counterclockwise around the origin;
-
, a rotation of clockwise around the origin;
-
, a reflection across the -axis; and
-
, a reflection across the -axis.
Each of these transformations maps the squares onto itself, but the positions of the labeled vertices will change. For example, applying and then would send the vertex at to and would send the vertex at to itself. How many sequences of transformations chosen from will send all of the labeled vertices back to their original positions? (For example, is one sequence of transformations that will send the vertices back to their original positions.)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Two different cubes of the same size are to be painted, with the color of each face being chosen independently and at random to be either black or white. What is the probability that after they are painted, the cubes can be rotated to be identical in appearance?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: How many positive integers satisfy
(Recall that is the greatest integer not exceeding .)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: What is the maximum value of for real values of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: How many integers are there such that whenever are complex numbers such that
then the numbers are equally spaced on the unit circle in the complex plane?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Let denote the number of ways of writing the positive integer as a product
where , the are integers strictly greater than , and the order in which the factors are listed matters (that is, two representations that differ only in the order of the factors are counted as distinct). For example, the number can be written as , and , so . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: For each real number with , let numbers and be chosen independently at random from the intervals and , respectively, and let be the probability that
What is the maximum value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions