¶ 1991 AMC8 Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 1991 AMC8 problems here.
Discussion Forum
Engage in discussion about the 1991 AMC8 math contest by visiting Random Math 1991 AMC8 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 1991 AMC8 problems, please refer below:
Problem 1:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: Two hundred thousand times two hundred thousand equals
Answer Choices:
A. four hundred thousand
B. four million
C. forty thousand
D. four hundred million
E. forty billion
Solution:
Problem 4: If , then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: A "domino" is made up of two small squares:
Which of the "checkerboards" illustrated below CANNOT be covered exactly and completely by a whole number of non-overlapping dominoes?
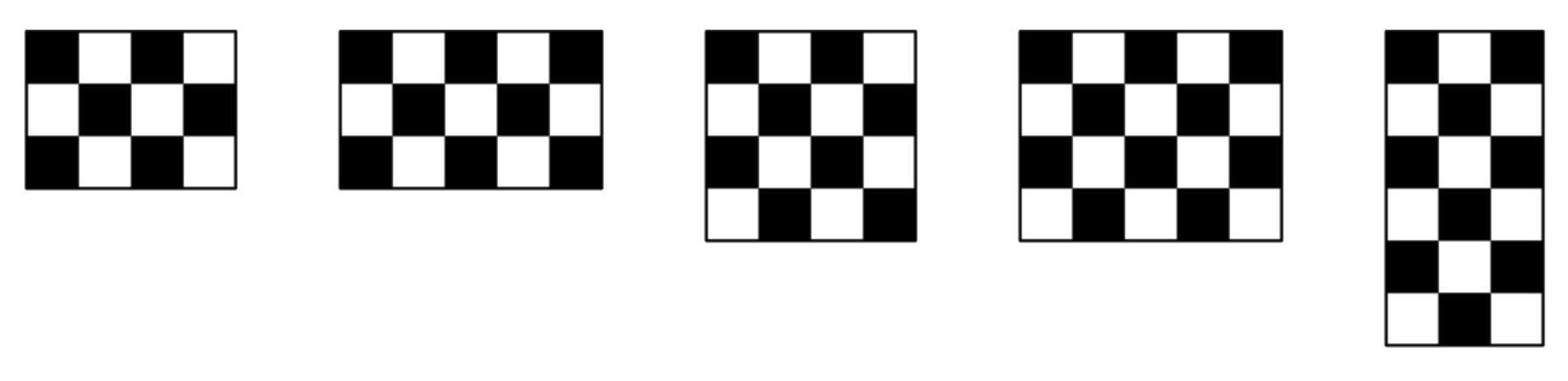
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: Which number in the array below is both the largest in its column and the smallest in its row? (Columns go up and down, rows go right and left.)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: The value of is closest to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: What is the largest quotient that can be formed using two numbers chosen from the set
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: How many whole numbers from through are divisible by either or or both?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: The area in square units of the region enclosed by parallelogram is
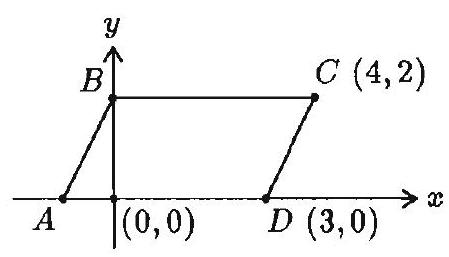
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: There are several sets of three different numbers whose sum is which can be chosen from . How many of these sets contain a
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: If , then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: How many zeros are at the end of the product
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Several students are competing in a series of three races. A student earns points for winning a race, point.s for finishing second and point for finishing third. There are no ties. What is the smallest number of points that a student must earn in the three races to be guaranteed of earning more points than any other student?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: All six sides of a rectangular solid were rectangles. A one-foot cube was cut out of the rectangular solid as shown. The total number of square feet in the surface of the new solid is how many more or less than that of the original solid?
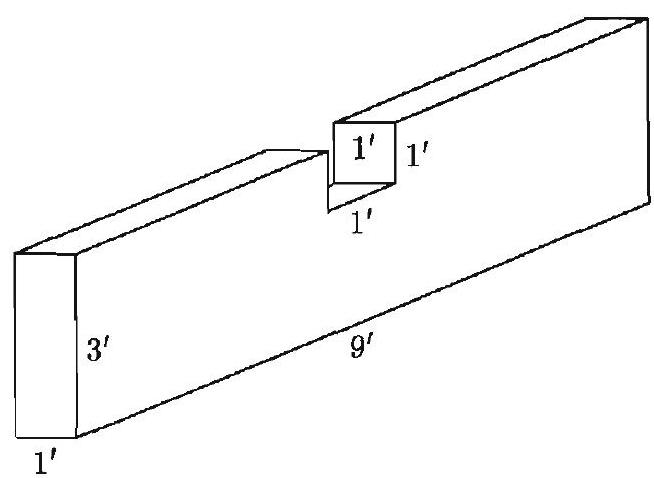
Answer Choices:
A. less
B. less
C. the same
D. more
E. more
Solution:
Problem 16: The squares on a piece of paper are numbered as shown in the diagram. While lying on a table, the paper is folded in half four times in the following sequence:
fold the top half over the bottom half
fold the bottom half over the top half
fold the right half over the left half
fold the left half over the right half.
Which numbered square is on top after step
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: An anditorium with rows of seats has seats in the first row. Each successive row has one more seat than the previous row. If students taking an exam are permitted to sit in any row, but not next to another student in that row, then the maximum number of students that can be seated for an exam is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: The vertical axis indicates the number of employees, but. the scale was accidentally omitled from this graph. What percent of the employees at the Gauss Company have worked there for years or more?
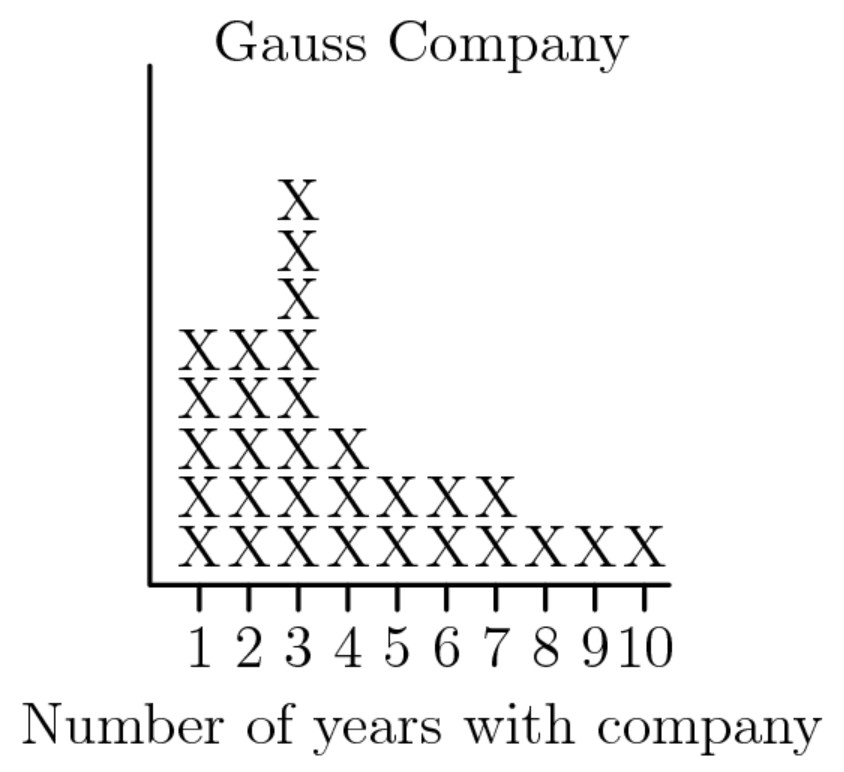
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: The average (arithmetic mean) of different positive whole numbers is . The largest possible value of any of these numbers is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: In the addition problem, each digit has been replaced
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: For every rise in itemperature, the volume of a certain gas expands by cubic centimeters. If the volume of the gas is cubic centimeters when the itemperature is , what was the volume of the gas in cubic centimeters when the itemperature was
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Each spinner is divided into equal parts. The results obtained from spinning the two spinners are multiplied. What is the probability that this product is an even number?
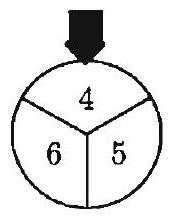
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: The Pythagoras High School band has female and male members. The Pythagoras High School orchestra has female and male members. There are females who are members in both band and orchestra. Altogether, there are students who are in either band or orchestra or both. The number of males in the band who are NOT in the orchestra is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: A cube of edge is cut into smaller cubes, not all the same size. If the edge of each of the smaller cubes is a whole number of centimeters, then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: An equilateral triangle is originally painted black. Each time the triangle is changed, the middle fourth of each black triangle turns white. After five changes, what fractional part of the original area of the black triangle remains black?
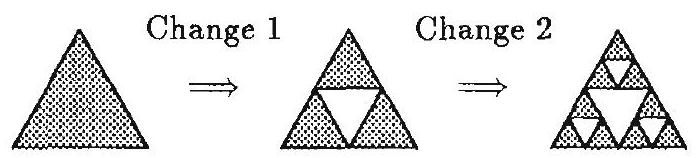
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions