¶ 2002 AMC8 Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2002 AMC8 problems here.
Discussion Forum
Engage in discussion about the 2002 AMC8 math contest by visiting Random Math 2002 AMC8 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2002 AMC8 problems, please refer below:
Problem 1: A circle and two distinct lines are drawn on a sheet of paper. What is the largest possible number of points of intersection of these figures?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: How many different combinations of bills and bills can be used to make a total of Order does not matter in this problem.
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: What is the smallest possible average of four distinct positive even integers?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: The year is a palindrome (a number that reads the same from left to right as it does from right to left). What is the product of the digits of the next year after that is a palindrome?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Carlos Montado was born on Saturday, November , . On what day of the week will Carlos be days old?
Answer Choices:
A. Monday
B. Wednesday
C. Friday
D. Saturday
E. Sunday
Solution:
Problem 6: A birdbath is designed to overflow so that it will be self-cleaning. Water flows in at the rate of milliliters per minute and drains at the rate of milliliters per minute. One of these graphs shows the volume of water in the birdbath during the filling time and continuing into the overflow time. Which one is it?

.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: The students in Mrs. Sawyer's class were asked to do a taste test of five kinds of candy. Each student chose one kind of candy. A bar graph of their preferences is shown. What percent of her class chose candy
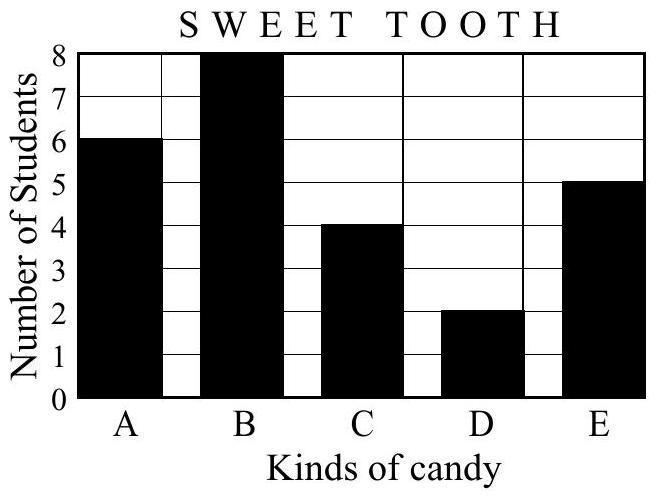
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Juan organizes the stamps in his collection by country and by the decade in which they were issued. The prices he paid for them at a stamp shop were: Brazil and France, each, Peru each, and Spain each. (Brazil and Peru are South Americal countries and France and Spain are in Europe.)
How many of his European stamps were issued in the
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: Juan organizes the stamps in his collection by country and by the decade in which they were issued. The prices he paid for them at a stamp shop were: Brazil and France, each, Peru each, and Spain each. (Brazil and Peru are South Americal countries and France and Spain are in Europe.)
His South American stamps issued before the cost him
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Juan organizes the stamps in his collection by country and by the decade in which they were issued. The prices he paid for them at a stamp shop were: Brazil and France, each, Peru each, and Spain each. (Brazil and Peru are South Americal countries and France and Spain are in Europe.)
The average price of his stamps is closest to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: A sequence of squares is made of identical square tiles. The edge of each square is one tile length longer than the edge of the previous square.
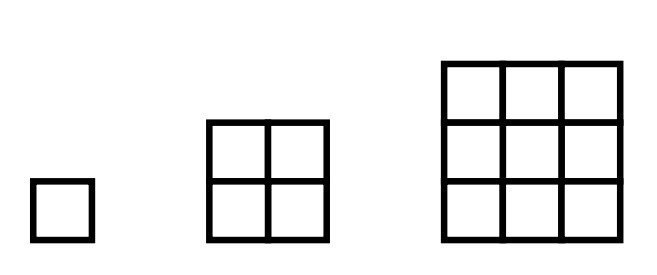
The first three squares are shown. How many more tiles does the seventh square require than the sixth?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: A board game spinner is divided into three regions labeled and . The probability of the arrow stopping on region is and on region is . The probability of the arrow stopping on region is
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: For his birthday, Bert gets a box that holds jellybeans when filled to capacity. A few weeks later, Carrie gets a larger box full of jellybeans. Her box is twice as high, twice as wide and twice as long as Bert's. Approximately, how many jellybeans did Carrie get?
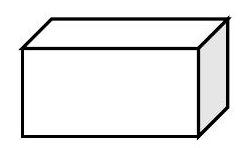
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: A merchant offers a large group of items at off. Later, the merchant takes off these sale prices and claims that the final price of these items is off the original price. The total discount is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: Which of the following polygons has the largest area?
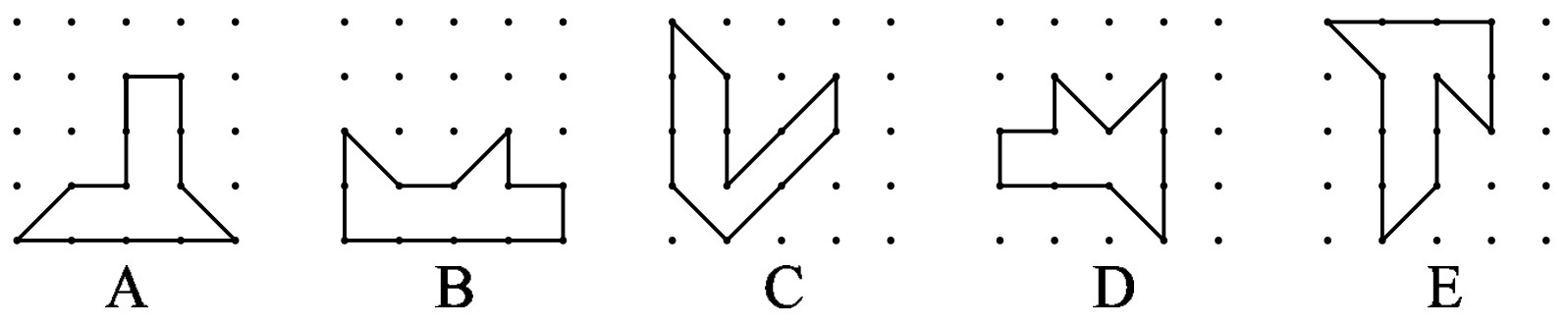
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: Right isosceles triangles are constructed on the sides of a right triangle, as shown. A capital letter represents the area of each triangle. Which one of the following is true?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: In a mathematics contest with ten problems, a student gains points for a correct answer and loses points for an incorrect answer. If Olivia answered every problem and her score was , how many correct answers did she have?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: Gage skated each day for days and each day for days. How long would he have to skate the ninth day in order to average minutes of skating each day for the entire time?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: How many whole numbers between and contain exactly one
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: The area of triangle is square inches. Points and are midpoints of congruent segments and . Altitude bisects . The area (in square inches) of the shaded region is
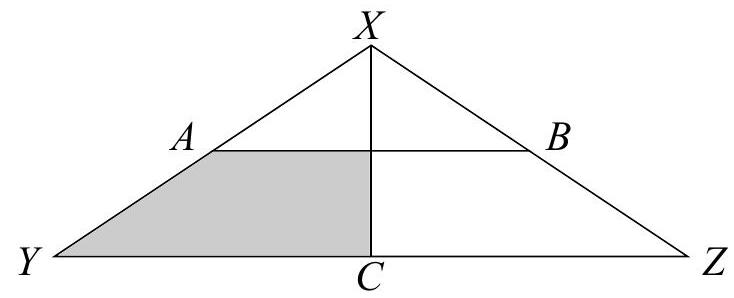
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Harold tosses a nickel four times. The probability that he gets at least as many heads as tails is

Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Six cubes, each an inch on an edge, are fastened together, as shown. Find the total surface area in square inches. Include the top, bottom and sides.
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: A corner of a tiled floor is shown. If the entire floor is tiled in this way and each of the four corners looks like this one, then what fraction of the tiled floor is made of darker tiles?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Miki has a dozen oranges of the same size and a dozen pears of the same size. Miki uses her juicer to extract ounces of pear juice from pears and ounces of orange juice from oranges. She makes a pear-orange juice blend from an equal number of pears and oranges. What percent of the blend is pear juice?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Loki, Moe, Nick and Ott are good friends. Ott had no money, but the others did. Moe gave Ott one-fifth of his money, Loki gave Ott one-fourth of his money and Nick gave Ott one-third of his money. Each gave Ott the same amount of money. What fractional part of the group's money does Ott now have?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions