¶ 2001 AMC8 Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2001 AMC8 problems here.
Discussion Forum
Engage in discussion about the 2001 AMC8 math contest by visiting Random Math 2001 AMC8 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2001 AMC8 problems, please refer below:
Problem 1: Casey's shop class is making a golf trophy. He has to paint dimples on a golf ball. If it takes him seconds to paint one dimple, how many minutes will he need to do his job?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: I'm thinking of two whole numbers. Their product is and their sum is . What is the larger number?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: Granny Smith has . Elberta has more than Anjou and Anjou has one-third as much as Granny Smith. How many dollars does Elberta have?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: The digits and are each used once to form the smallest possible even five-digit number. The digit in the tens place is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: On a dark and stormy night Snoopy suddenly saw a flash of lightning. Ten seconds later he heard the sound of thunder. The speed of sound is feet per second and one mile is feet. Estimate, to the nearest halfmile, how far Snoopy was from the flash of lightning.

Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: Six trees are equally spaced along one side of a straight road. The distance from the first tree to the fourth is feet. What is the distance in feet between the first and last trees?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: To promote her school's annual Kite Olympics, Genevieve makes a small kite and a large kite for a bulletin board display. The kites look like the one in the diagram. For her small kite Genevieve draws the kite on a one-inch grid. For the large kite she triples both the height and width of the entire grid.
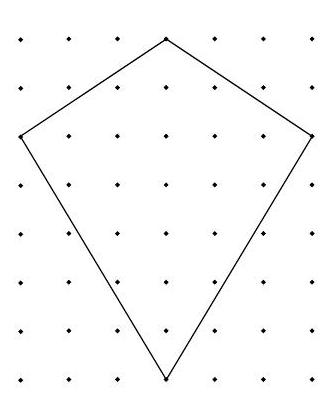
What is the number of square inches in the area of the small kite?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: To promote her school's annual Kite Olympics, Genevieve makes a small kite and a large kite for a bulletin board display. The kites look like the one in the diagram. For her small kite Genevieve draws the kite on a one-inch grid. For the large kite she triples both the height and width of the entire grid.

Genevieve puts bracing on her large kite in the form of a cross connecting opposite corners of the kite. How many inches of bracing material does she need?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: To promote her school's annual Kite Olympics, Genevieve makes a small kite and a large kite for a bulletin board display. The kites look like the one in the diagram. For her small kite Genevieve draws the kite on a one-inch grid. For the large kite she triples both the height and width of the entire grid.

The large kite is covered with gold foil. The foil is cut from a rectangular piece that just covers the entire grid. How many square inches of waste material are cut off from the four corners?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: A collector offers to buy state quarters for of their face value. At that rate how much will Bryden get for his four state quarters?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: Points and have these coordinates: , , and . The area of quadrilateral is
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: If , then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Of the students in Richelle's class, prefer chocolate pie, prefer apple, and prefer blueberry. Half of the remaining students prefer cherry pie and half prefer lemon. For Richelle's pie graph showing this data, how many degrees should she use for cherry pie?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Tyler has entered a buffet line in which he chooses one kind of meat, two different vegetables and one dessert. If the order of food items is not important, how many different meals might he choose?
-
Meat: beef, chicken, pork.
-
Vegetables: baked beans, corn, potatoes, tomatoes.
-
Dessert: brownies, chocolate cake, chocolate pudding, ice cream.
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: Homer began peeling a pile of potatoes at the rate of potatoes per minute. Four minutes later Christen joined him and peeled at the rate of potatoes per minute. When they finished, how many potatoes had Christen peeled?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: A square piece of paper, inches on a side, is folded in half vertically. Both layers are then cut in half parallel to the fold. Three new rectangles are formed, a large one and two small ones. What is the ratio of the perimeter of one of the small rectangles to the perimeter of the large rectangle
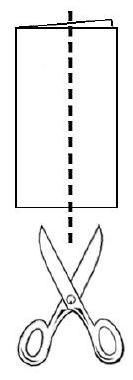
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: For the game show Who Wants To Be A Millionaire?, the dollar values of each question are shown in the following table (where .
Between which two questions is the percent increase of the value the smallest?
Answer Choices:
A. From to
B. From to
C. From to
D. From to
E. From to
Solution:
Problem 18: Two dice are thrown. What is the probability that the product of the two numbers is a multiple of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: Car traveled at a constant speed for a given time. This is shown by the dashed line. Car traveled at twice the speed for the same distance. If Car 's speed and time are shown as solid line, which graph illustrates this?
Answer Choices:
A.
.jpg)
.jpg)
.jpg)
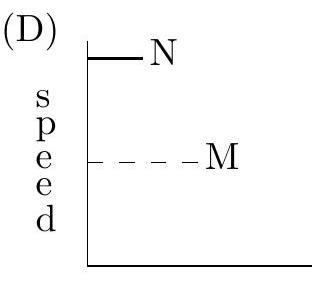
.jpg)
Solution:
Problem 20: Kaleana shows her test score to Quay, Marty and Shana, but the others keep theirs hidden. Quay thinks, "At least two of us have the same score." Marty thinks, "I didn't get the lowest score." Shana thinks, "I didn't get the highest score." List the scores from lowest to highest for Marty , Quay and Shana .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: The mean of a set of five different positive integers is . The median is . The maximum possible value of the largest of these five integers is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: On a twenty-question test, each correct answer is worth points, each unanswered question is worth point and each incorrect answer is worth points. Which of the following scores is NOT possible?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: Points and are vertices of an equilateral triangle, and points and are midpoints of its sides. How many noncongruent triangles can be drawn using any three of these six points as vertices?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Each half of this figure is composed of red triangles, blue triangles and white triangles. When the upper half is folded down over the centerline, pairs of red triangles coincide, as do pairs of blue triangles. There are red-white pairs. How many white pairs coincide?
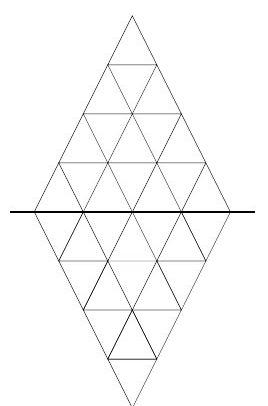
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: There are four-digit whole numbers that use each of the four digits and 7 exactly once. Only one of these four-digit numbers is a multiple of another one. Which of the following is it?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions