¶ 2000 AMC8 Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2000 AMC8 problems here.
Discussion Forum
Engage in discussion about the 2000 AMC8 math contest by visiting Random Math 2000 AMC8 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2000 AMC8 problems, please refer below:
Problem 1: Aunt Anna is years old. Caitlin is years younger than Brianna, and Brianna is half as old as Aunt Anna. How old is Caitlin?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: Which of these numbers is less than its reciprocal?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: How many whole numbers lie in the interval between and
Answer Choices:
A.
B.
C.
D.
E. infinitely many
Solution:
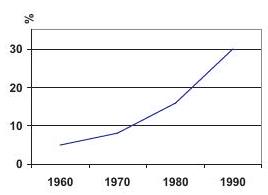
Problem 4: In only of the working adults in Carlin City worked at home. By the "at-home" work force had increased to . In there were approximately working at home, and in there were . The graph that best illustrates this is:
Answer Choices:
A.
.jpg)
B.
.jpg)
C.
.jpg)
D.
.jpg)
E.
Solution:
Problem 5: Each principal of Lincoln High School serves exactly one -year term. What is the maximum number of principals this school could have during an -year period?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: Figure is a square. Inside this square three smaller squares are drawn with side lengths as labeled. the area of the shaded L-shaped region is
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: What is the minimum possible product of three different numbers of the set
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Three dice with faces numbered through are stacked as shown. Seven of the eighteen faces are visible, leaving eleven faces hidden(back, bottom, between). The total number of dots NOT visible in this view is
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
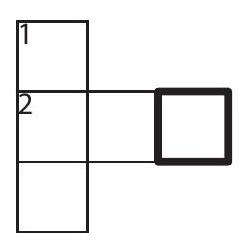
Problem 9: Three-digit powers of and are used in this cross-number puzzle. What is the only possible digit for the outlined square?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Ara and Shea were once the same height. Since then Shea has grown while Ara has grown half as many inches as Shea. Shea is now inches tall. How tall, in inches, is Ara now?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: The number has the property that it is divisible by its units digit. How many whole numbers between and have this property?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: A block wall feet long and feet high will be constructed using blocks that are foot high and either feet long or foot long (no blocks may be cut). The vertical joins in the blocks must be staggered as shown, and the wall must be even on the ends. What is the smallest number of blocks needed to build this wall?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: In triangle , we have and . If bisects , then
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: What is the units digit of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
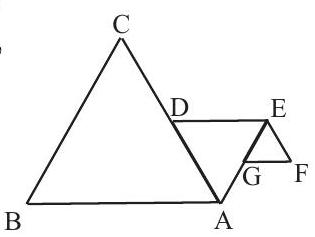
Problem 15: Triangle , , and are all equilateral. Points and are midpoints of and , respectively. If , what is the perimeter of figure
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: In order for Mateen to walk a kilometer in his rectangular backyard, he must walk the length times or walk its perimeter times. What is the area of Mateen's backyard in square meters?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: The operation is defined for all nonzero numbers by . Determine .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
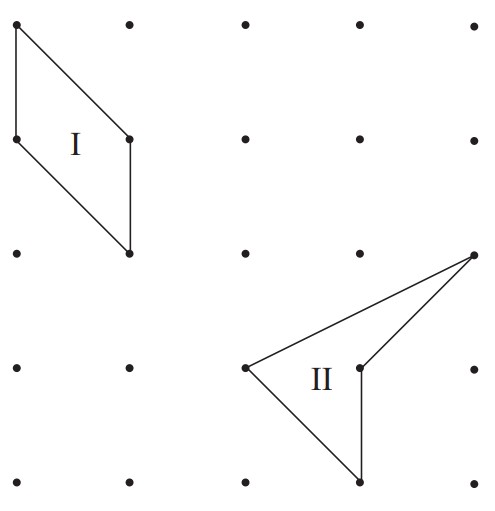
Problem 18: Consider these two geoboard quadrilaterals. Which of the following statements is true?
Answer Choices:
A. The area of quadrilateral is more than the area of quadrilateral .
B. The area of quadrilateral is less than the area of quadrilateral .
C. The quadrilaterals have the same area and the same perimeter.
D. The quadrilaterals have the same area, but the perimeter of is more than the perimeter of .
E. The quadrilaterals have the same area, but the perimeter of is less than the perimeter of .
Solution:
Problem 19: Three circular arcs of radius units bound the region shown. Arcs and are quarter-circles, and arc is a semicircle. What is the area, in square units, of the region?
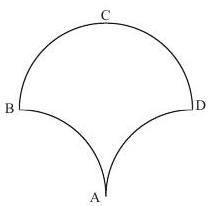
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: You have nine coins: a collection of pennies, nickels, dimes, and quarters having a total value of , with at least one coin of each type. How many dimes must you have?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Keiko tosses one penny and Ephraim tosses two pennies. The probability that Ephraim gets the same number of heads that Keiko gets is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: A cube has edge length . Suppose that we glue a cube of edge length on top of the big cube so that one of its faces rests entirely on the top face of the larger cube. The percent increase in the surface area (sides, top, and bottom) from the original cube to the new solid formed is closest to:
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: There is a list of seven numbers. The average of the first four numbers is , and the average of the last four numbers is . If the average of all seven numbers is , then the number common to both sets of four numbers is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: If and , Then
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: The area of rectangle is . If point and the midpoints of and are joined to form a triangle, the area of that triangle is
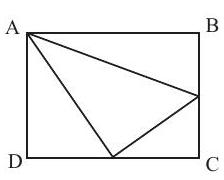
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions