¶ 2011 AMC8 Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2011 AMC8 problems here.
Discussion Forum
Engage in discussion about the 2011 AMC8 math contest by visiting Random Math 2011 AMC8 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2011 AMC8 problems, please refer below:
Problem 1: Margie bought apples at a cost of cents per apple. She paid with a -dollar bill. How much change did Margie receive?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: Karl's rectangular vegetable garden is feet by feet, and Makenna's is feet by feet. Whose garden is larger in area?
Answer Choices:
A. Karl's garden is larger by square feet.
B. Karl's garden is larger by square feet.
C. The gardens are the same size.
D. Makenna's garden is larger by square feet.
E. Makenna's garden is larger by square feet.
Solution:
Problem 3: Extend the square pattern of black and white square tiles by attaching a border of black tiles around the square. What is the ratio of black tiles to white tiles in the extended pattern?

Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Here is a list of the numbers of fish that Tyler caught in nine outings last summer:
Which statement about the mean, mode, and median of these numbers is true?
Answer Choices:
A. median mean mode
B. mean mode median
C. mean median mode
D. median mode mean
E. mode median mean
Solution:
Problem 5: What time was it minutes after the beginning of January ,
.jpg)
Answer Choices:
A. January at PM
B. January at PM
C. January at AM
D. January at AM
E. January at PM
Solution:
Problem 6: In a town of adults, every adult owns a car, a motorcycle, or both. If adults own cars, and adults own motorcycles, how many of the car owners do not own a motorcycle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: Each of the following four large congruent squares is subdivided into combinations of congruent triangles or rectangles and is partially shaded. What percent of the total area is partially shaded?
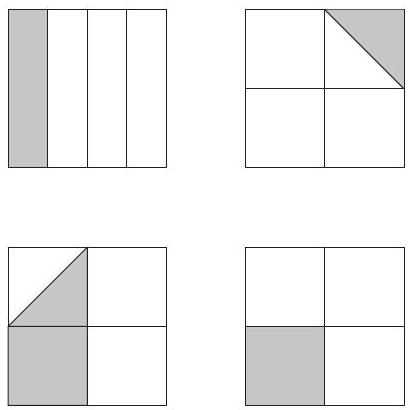
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Bag contains three chips labeled , and . Bag contains three chips labeled , and . If one chip is drawn from each bag, how many different values are possible for the sum of the two numbers on the chips?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: Carmen takes a long bike ride on a hilly highway. The graph indicates the miles traveled during the time of her ride. What is Carmen's average speed for her entire ride in miles per hour?
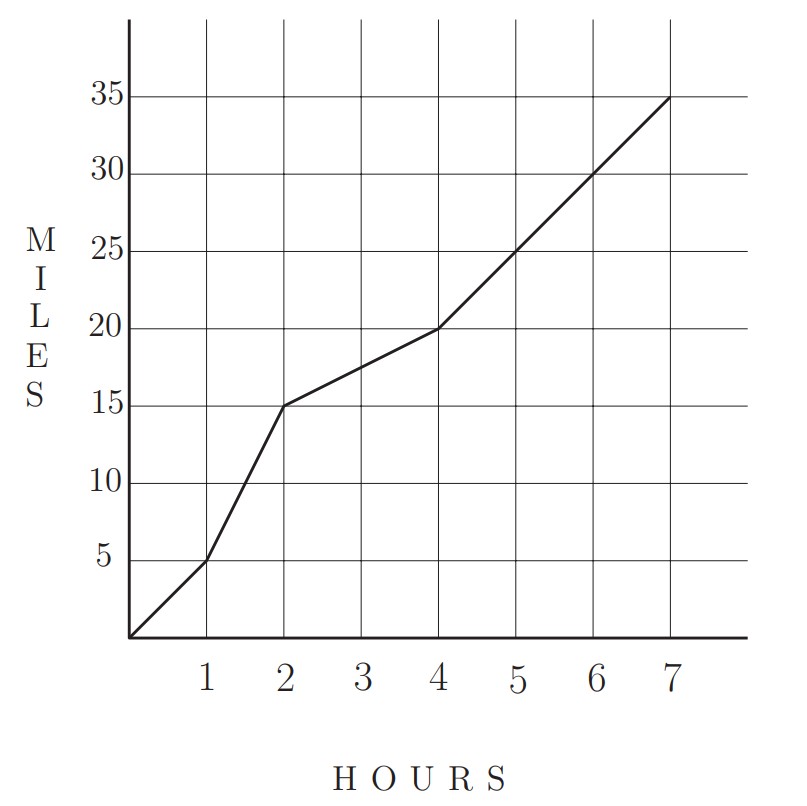
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: The taxi fare in Gotham City is for the first mile and additional mileage charged at the rate for each additional mile. You plan to give the driver a tip. How many miles can you ride for

Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: The graph below shows the number of minutes studied by both Asha (black bar) and Sasha (grey bar) in one week. On the average, how many more minutes per day did Sasha study than Asha?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: Angie, Bridget, Carlos, and Diego are seated at random around a square table, one person to a side. What is the probability that Angie and Carlos are seated opposite each other?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Two congruent squares, and , have side length . They overlap to form the by rectangle shown. What percent of the area of rectangle is shaded?
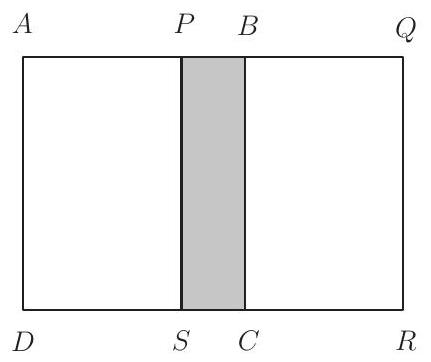
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: There are students at Colfax Middle School, where the ratio of boys to girls is . There are students at Winthrop Middle School, where the ratio of boys to girls is . The two schools hold a dance and all students from both schools attend. What fraction of the students at the dance are girls?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: How many digits are in the product
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: Let be the area of a triangle with sides of length , and . Let be the area of a triangle with sides of length , and . What is the relationship between and
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Let , and be whole numbers. If , then what does equal?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: A fair six-sided die is rolled twice. What is the probability that the first number that comes up is greater than or equal to the second number?

Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: How many rectangles are in this figure?
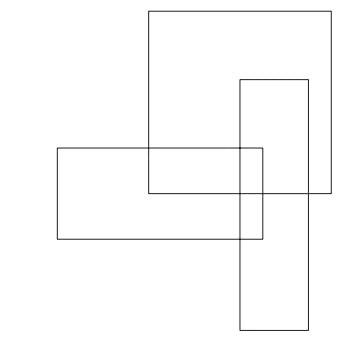
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Quadrilateral is a trapezoid, , and the altitude is . What is the area of the trapezoid?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Students guess that Norb's age is , and . Norb says, "At least half of you guessed too low, two of you are off by one and my age is a prime number." How old is Norb?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: What is the tens digit of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: How many -digit positive integers have four different digits, where the leading digit is not zero, the integer is a multiple of , and is the largest digit?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: In how many ways can be written as the sum of two primes?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: A circle with radius is inscribed in a square and circumscribed about another square as shown. Which fraction is closest to the ratio of the circle's shaded area to the shaded area between the two squares?
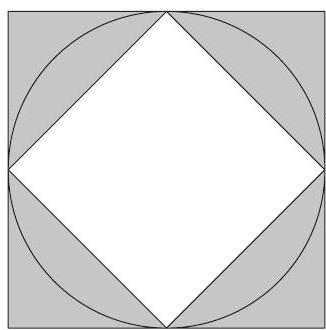
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions