¶ 2010 AMC8 Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2010 AMC8 problems here.
Discussion Forum
Engage in discussion about the 2010 AMC8 math contest by visiting Random Math 2010 AMC8 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2010 AMC8 problems, please refer below:
Problem 1: At Euclid Middle School the mathematics teachers are Miss Germain, Mr. Newton, and Mrs. Young. There are students in Miss Germain's class, students in Mr. Newton's class, and students in Mrs. Young's class taking the Contest this year. How many mathematics students at Euclid Middle School are taking the contest?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: If for positive integers, then what is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: The graph shows the price of five gallons of gasoline during the first ten months of the year. By what percent is the highest price more than the lowest price?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: What is the sum of the mean, median, and mode of the numbers
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Alice needs to replace a light bulb located centimeters below the ceiling in her kitchen. The ceiling is meters above the floor. Alice is meters tall and can reach centimeters above the top of her head. Standing on a stool, she can just reach the light bulb. What is the height of the stool, in centimeters?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: Which of the following figures has the greatest number of lines of symmetry?
Answer Choices:
A. equilateral triangle
B. non-square rhombus
C. non-square rectangle
D. isosceles trapezoid
E. square
Solution:
Problem 7: Using only pennies, nickels, dimes, and quarters, what is the smallest number of coins Freddie would need so he could pay any amount of money less than a dollar?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: As Emily is riding her bicycle on a long straight road, she spots Emerson skating in the same direction mile in front of her. After she passes him, she can see him in her rear view mirror until he is mile behind her. Emily rides at a constant rate of miles per hour, and Emerson skates at a constant rate of miles per hour. For how many minutes can Emily see Emerson?

Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: Ryan got of the problems correct on a -problem test, on a -problem test, and on a -problem test. What percent of all the problems did Ryan answer correctly?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Six pepperoni circles will exactly fit across the diameter of a -inch pizza when placed as shown. If a total of circles of pepperoni are placed on this pizza without overlap, what fraction of the pizza is covered by pepperoni?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: The top of one tree is feet higher than the top of another tree. The heights of the two trees are in the ratio . In feet, how tall is the taller tree?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: Of the balls in a large bag, are red and the rest are blue. How many of the red balls must be removed from the bag so that of the remaining balls are red?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: The lengths of the sides of a triangle measured in inches are three consecutive integers. The length of the shortest side is of the perimeter. What is the length of the longest side?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: What is the sum of the prime factors of
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: A jar contains five different colors of gum drops: are blue, are brown, are red, are yellow, and the other gum drops are green. If half of the blue gum drops are replaced by brown gum drops, how many of the gum drops will be brown?

Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: A square and a circle have the same area. What is the ratio of the side length of the square to the radius of the circle?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: The diagram shows an octagon consisting of unit squares. The portion below is a unit square and a triangle with base . If bisects the area of the octagon, what is the ratio
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: A decorative window is made up of a rectangle with semicircles on either end. The ratio of to is and inches. What is the ratio of the area of the rectangle to the combined areas of the semicircles?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
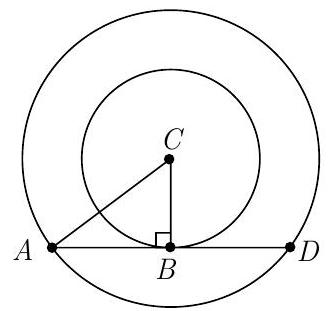
Problem 19: The two circles pictured have the same center . Chord is tangent to the inner circle at is , and chord has length . What is the area between the two circles?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: In a room, of all the people are wearing gloves, and of the people are wearing hats. What is the minimum number of people in the room wearing both a hat and gloves?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Hui is an avid reader. She bought a copy of the bestseller Math is Beautiful. On the first day, Hui read of the pages plus more, and on the second day she read of the remaining pages, plus pages. On the third day, she read of the remaining pages, plus pages. She then realized that there were only pages left to read, which she read the next day. How many pages are in this book?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: The hundreds digit of a three-digit number is more than the units digit. The digits of the three-digit number are reversed, and the result is subtracted from the original three-digit number. What is the units digit of the result?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
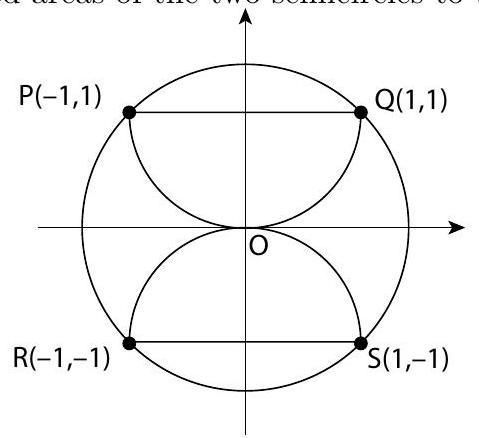
Problem 23: Semicircles and pass through the center of circle . What is the ratio of the combined areas of the two semicircles to the area of the circle
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: What is the correct ordering of the three numbers , and
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Every day at school, Jo climbs a flight of stairs. Jo can take stairs , or at a time. For example, Jo could climb , then , then stairs. In how many ways can Jo climb the stairs?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions