¶ 1972 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1972 AHSME problems, please refer below:
Problem 1: The lengths in inches of the three sides of each of four triangles I, II, III, and IV are as follows:
I , and
II , and
III , and
IV , and
Of these four given triangles, the only right triangles are
Answer Choices:
A. I and II
B. I and III
C. I and IV
D. I, II, and III
E. I, II, and IV
Solution:
Problem 2: If a dealer could get his goods for less while keeping his selling price fixed, his profit, based on cost, would be increased to from his present profit of which is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: If where , then is equal to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: The number of solutions to where X is a subset of is
Answer Choices:
A.
B.
C.
D.
E. None of these
Solution:
Problem 5: From among those which have the greatest and the next to the greatest values in that order, are
Answer Choices:
A.
B.
C.
D.
E. None of these
Solution:
Problem 6: If , then the value of is
Answer Choices:
A. 1 only
B. 5 only
C. 1 or 5
D.
E.
Solution:
Problem 7: If , then is equal to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: If where and are real, then
Answer Choices:
A.
B.
C. and
D.
E. None of these
Solution:
Problem 9: Ann and Sue bought identical boxes of stationery. Ann used hers to write 1-sheet letters and Sue used hers to write 3-sheet letters. Ann used all the envelopes and had 50 sheets of paper left, while Sue used all of the sheets of paper and had 50 envelopes left. The number of sheets of paper in each box was
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: For real, the inequality is equivalent to
Answer Choices:
A. or
B.
C.
D. or
E. or
Solution:
Problem 11: The value(s) of for which the following pair of equations
may have a real common solution, are
Answer Choices:
A. 4 only
B.
C.
D. none of these
E. all y
Solution:
Problem 12: The number of cubic feet in the volume of a cube is the same as the number of square inches in its surface area. The length of the edge expressed as a number of feet is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Inside square ABCD (See figure) with sides of length 12 inches, segment AE is drawn where is the point on DC which is 5 inches from . The perpendicular bisector of AE is drawn and intersects AE, AD, and BC at points M, P, and Q respectively. The ratio of segment PM to MQ is
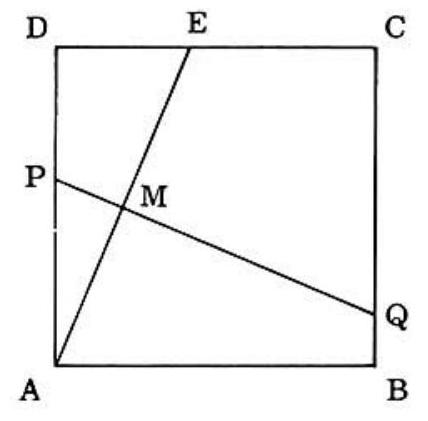
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: A triangle has angles of and . If the side opposite the angle has length 8, then the side opposite the angle has length
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: A contractor estimated that one of his two bricklayers would take 9 hours to build a certain wall and the other 10 hours. However, he knew from experience that when they worked together, their combined output fell by 10 bricks per hour. Being in a hurry, he put both men on the job and found that it took exactly 5 hours to build the wall. The number of bricks in the wall was
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: There are two positive numbers that may be inserted between 3 and 9 such that the first three are in geometric progression while the last three are in arithmetic progression. The sum of those two positive numbers is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: A piece of string is cut in two at a point selected at random. The probability that the longer piece is at least times as large as the shorter piece is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: Let be a trapezoid with the measure of base twice that of base , and let be the point of intersection of the diagonals. If the measure of diagonal AC is 11, then that of segment EC is equal to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: The sum of the first terms of the sequence in terms of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: If where and , then is equal to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: If the sum of the measures in degrees of angles A, B, C, D, E , and F in the figure to the right is , then is equal to
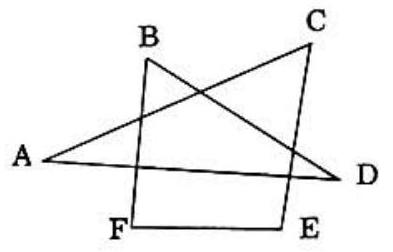
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: If are imaginary roots of the equation where , and are real numbers, then in terms of and is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: The radius of the smallest circle containing the symmetric figure composed of the 3 unit squares shown at the right is
.jpg)
Answer Choices:
A.
B.
C.
D.
E. None of these
Solution:
Problem 24: A man walked a certain distance at a constant rate. If he had gone mile per hour faster, he would have walked the distance in four-fifths of the time; if he had gone mile per hour slower, he would have been hours longer on the road. The distance in miles he walked was
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Inscribed in a circle is a quadrilateral having sides of lengths , and 60 taken consecutively. The diameter of this circle has length
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 26: In the circle to the right, is the mid-point of arc CAB and segment MP is perpendicular to chord at . If the measure of chord is and that of segment AP is , then segment PB has measure equal to
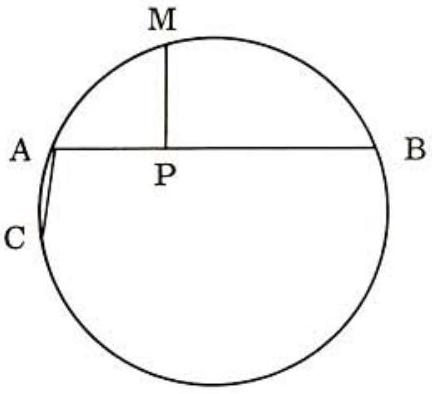
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 27: If the area of is 64 square inches and the geometric mean (mean proportional) between sides AB and AC is 12 inches, then is equal to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 28: A circular disc with diameter is placed on an checkerboard with width D so that the centers coincide. The number of checkerboard squares which are completely covered by the disc is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 29: If for , then in terms of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 30: A rectangular piece of paper 6 inches wide is folded as in the diagram so that one corner touches the opposite side. The length in inches of the crease in terms of angle is
.jpg)
Answer Choices:
A.
B.
C.
D.
E. None of these
Solution:
Problem 31: When the number is divided by 13 , the remainder in the division is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 32: Chords and in the circle to the right intersect at E and are perpendicular to each other. If segments AE, EB, and ED have measures 2, 6, and 3 respectively, then the length of the diameter of the circle is
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 33: The minimum value of the quotient of a (base ten) number of three different nonzero digits divided by the sum of its digits is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 34: Three times Dick's age plus Tom's age equals twice Harry's age. Double the cube of Harry's age is equal to three times the cube of Dick's age added to the cube of Tom's age. Their respective ages are relatively prime to each other. The sum of the squares of their ages is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 35: Equilateral triangle ABP (See figure) with side of length 2 inches is placed inside square AXYZ with side of length 4 inches so that B is on side AX. The triangle is rotated clockwise about , then P , and so on along the sides of the square until P returns to its original position. The length of the path in inches traversed by vertex is equal to
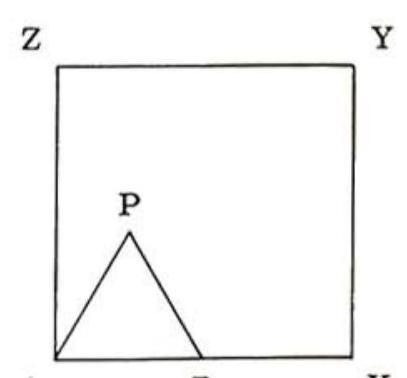
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions