¶ 1973 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1973 AHSME problems, please refer below:
Problem 1: A chord which is the perpendicular bisector of a radius of length 12 in a circle, has length
Answer Choices:
A.
B.
C.
D.
E. None of these
Solution:
Problem 2: One thousand unit cubes are fastened together to form a large cube with edges of 10 units which is painted then separated into the original cubes. The number of these unit cubes which have at least one face painted is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: The stronger Goldbach conjecture states that any even whole number greater than 7 can be written as the sum of exactly two different prime numbers. For such representation of even number 126, the largest difference between the two primes is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Two congruent triangles are placed so that they overlap partly and their hypotenuses coincide. If the hypotenuse of each triangle is 12, the area common to both triangles is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Of the following five statements, I to V, about the binary operation of averaging (arithmetic mean),
I. Averaging is associative
II. Averaging is commutative
III. Averaging distributes over addition
IV. Addition distributes over averaging
V. Averaging has an identity element
those which are always true, are
Answer Choices:
A. All
B. I and II only
C. II and III only
D. II and IV only
E. II and V only
Solution:
Problem 6: In a certain scale of notation, the square of 24 is represented by 554. The base of this scale is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: The sum of all the integers between 50 and 350 which end in 1, is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: If 1 pint of paint is needed to paint a statue 6 ft. high, then the number of pints it will take to paint (to the same thickness) 540 copies 1 ft. high, is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: In with right angle at , altitude and median trisect the right angle. If the area of is , then the area of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: If is a real number, then the simultaneous system has no solution if and only if is equal to
Answer Choices:
A.
B.
C.
D. 0 or 1
E.
Solution:
Problem 11: A circle with a circumscribed and an inscribed square centered at the origin 0 of a rectangular coordinate system with positive and axes OX and OY, is shown in each figure I to IV below
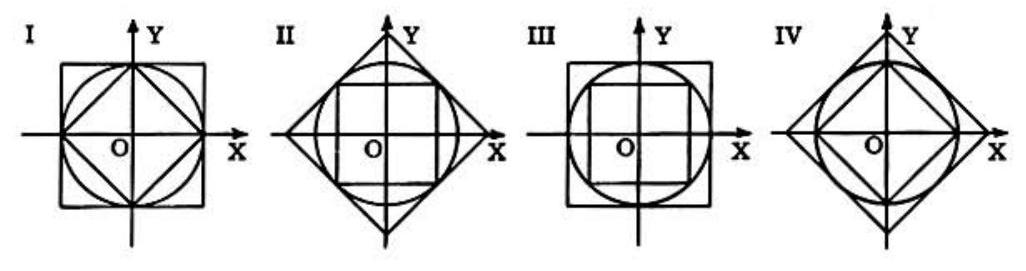
The inequalities
are represented geometrically by the figure numbered
Answer Choices:
A.
B.
C.
D.
E. None of these
Solution:
Problem 12: The average (arithmetic mean) age of a group consisting of doctors and lawyers is 40. If the doctors average 35 and the lawyers 50 years old, then the ratio of the number of doctors to the number of lawyers is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: The fraction is equal to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: Each valve A, B, and C, when open, releases water into a tank at its own constant rate. The number of hours required with only valves and open is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: A sector with acute central angle is cut from a circle of radius 6. The radius of the circle circumscribed about the sector is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: If the sum of all the angles except one of a convex polygon is , then the number of sides of the polygon must be
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: If is an acute angle and , then equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: If is a prime number, then 24 divides without remainder
Answer Choices:
A.
B. Sometimes only
C.
D. only if
E. None of these
Solution:
Problem 19: Define for and a positive to be
where is the greatest integer for which . Then the quotient ! is equal to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: A cowboy is 4 miles south of a stream which flows due east. He is also 8 miles west and 7 miles north of his cabin. The shortest distance (in miles) he can travel and accomplish this is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: The number of sets of two or more consecutive positive integers whose sum is 100, is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: The set of all real solutions of the inequality is
Answer Choices:
A.
B.
C.
D.
E. (empty)
Solution:
Problem 23: There are two cards; one is red on both sides and the other is red on one side and blue on the other. The cards have the same probability () of being chosen, and one is chosen and placed on the table. If the upper-side of the card on the table is red, then the probability that the under-side is also red, is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: The check for a luncheon of 3 sandwiches, 7 cups of coffee and one piece of pie came to . The check for a luncheon consisting of 4 sandwiches, 10 cups of coffee and one piece of pie came to at the same place. The cost of a luncheon consisting of one sandwich, one cup of coffee and one piece of pie at the same place will come to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: A circular grass plot 12 feet in diameter is cut by a straight gravel path 3 feet wide, one edge of which passes through the center of the plot. The number of square feet in the remaining grass area is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 26: The number of terms in an A.P. (Arithmetic Progression) is even. The sums of the odd and even numbered terms are 24 and 30 respectively. If the last term exceeds the first by , the number of terms in the A.P. is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 27: Cars A and B travel the same distance. Car A travels half that distance at miles per hour and half at miles per hour. Car B travels half the time at miles per hour and half at miles per hour. The average speed of Car A is miles per hour and that of Car B is miles per hour: Then we always have
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 28: If , and are in geometric progression (G.P.) with and is an integer, then form a sequence
Answer Choices:
A. which is a G.P.
B. which is an arithmetic progression (A.P.)
C. in which the reciprocals of the terms form an A.P.
D. in which the second and third terms are the powers of the first and second respectively
E. None of these
Solution:
Problem 29: Two boys start moving from the same point on a circular track but in opposite directions. Their speeds are 5 ft per sec and 9 ft per sec. If they start at the same time and finish when they first meet at the point again, then the number of times they meet between the start and finish is
Answer Choices:
A.
B.
C.
D. infinitely many
E. None of these
Solution:
Problem 30: Let denote the greatest integer where and where . Then we have
Answer Choices:
A. The point does not belong to for any .
B. The area of is bounded by 0 and .
C. is contained in the first quadrant for all .
D. The center of for any is on the line .
E. None of the other statements is true.
Solution:
Problem 31: In the following equation, each of the letters represents uniquely a different digit and in base ten, (YE) - (ME) TTT with the number YE less than ME in the product on the left. The sum equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 32: The volume of a regular pyramid whose base is an equilateral triangle of side length 6 and whose other edges are each of length , is
Answer Choices:
A.
B.
C.
D.
E. None of these
Solution:
Problem 33: When one ounce of water is added to a mixture of acid and water, the new mixture is acid. When one ounce of acid is added to the new mixture, the result is acid. The percentage of acid in the original mixture is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 34: A plane flew straight against a wind between two towns in 84 minutes and returned with that wind in 9 minutes less than it would take in still air. The number of minutes (2 answers) for the return trip was
Answer Choices:
A. 54 or 18
B. 60 or 15
C. 63 or 12
D. 72 or 36
E. 75 or 20
Solution:
Problem 35: In the unit circle shown in the figure to the right, chords and are parallel to the unit radius OR of the circle with center at 0. Chords MP, PQ and NR are each units long and chord MN is d units long. Of the three equations
I. ,
II. ds ,
III.
those which are necessarily true are
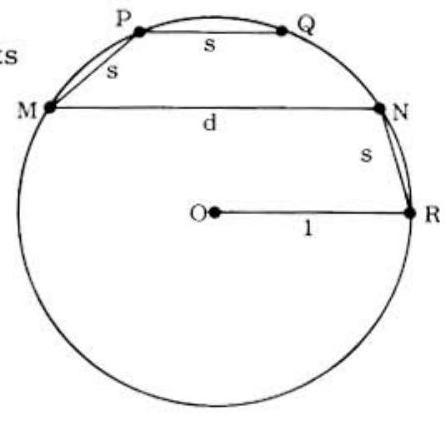
Answer Choices:
A. I only
B. II only
C. III only
D. I and II only
E. I, II, and III
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions