ΒΆ 1974 AHSME Problems and SolutionsIndividual Problems and Solutions
For problems and detailed solutions to each of the 1974 AHSME problems, please refer below:
Problem 1: If x β 0 x ξ = 0 y β 0 y ξ = 0 2 x + 3 y = 1 2 x 2 β + y 3 β = 2 1 β
Answer Choices:
A. 4 x + 3 y = x y 4 x + 3 y = x y y = 4 x 6 β y y = 6 β y 4 x β x 2 + y 3 = 2 2 x β + 3 y β = 2 4 y y β 6 = x y β 6 4 y β = x
Solution:
View Solution
Problem 2: Let x 1 x 1 β x 2 x 2 β x 1 β x 2 x 1 β ξ = x 2 β 3 x i 2 β h x i = b , i = 1 , 2 3 x i 2 β β h x i β = b , i = 1 , 2 x 1 + x 2 x 1 β + x 2 β
Answer Choices:
A. β h 3 β 3 h β h 3 3 h β b 3 3 b β 2 b 2 b β b 3 β 3 b β
Solution:
View Solution
Problem 3: The coefficient of x 7 x 7 ( 1 + 2 x β x 2 ) 4 ( 1 + 2 x β x 2 ) 4
Answer Choices:
A. β 8 β 8 12 1 2 6 6 β 12 β 1 2
Solution:
View Solution
Problem 4: What is the remainder when x 51 + 51 x 5 1 + 5 1 x + 1 x + 1
Answer Choices:
A. 0 0 1 1 49 4 9 50 5 0 51 5 1
Solution:
View Solution
Problem 5: Given a quadrilateral A B C D A B C D A B A B B B E E β B A D = 9 2 β β B A D = 9 2 β β A D C = 6 8 β β A D C = 6 8 β β E B C β E B C
Answer Choices:
A. 6 6 β 6 6 β 6 8 β 6 8 β 7 0 β 7 0 β 8 8 β 8 8 β 9 2 β 9 2 β
Solution:
View Solution
Problem 6: For positive real numbers x x y y x β y = x β
y x + y x β y = x + y x β
y β
Answer Choices:
A. β β β β β β β β
Solution:
View Solution
Problem 7: A town's population increased by 1,200 people, and then this new population decreased by 11 % 1 1 %
Answer Choices:
A. 1200 1 2 0 0 11200 1 1 2 0 0 9968 9 9 6 8 10000 1 0 0 0 0
Solution:
View Solution
Problem 8: What is the smallest prime number dividing the sum 3 11 + 5 13 3 1 1 + 5 1 3
Answer Choices:
A. 2 2 3 3 5 5 3 11 + 5 13 3 1 1 + 5 1 3
Solution:
View Solution
Problem 9: The integers greater than one are arranged in five columns as follows:
2 3 4 5 9 8 7 6 10 11 12 13 17 16 15 14 β
β
β
β
9 1 7 β 2 8 1 0 1 6 β
β 3 7 1 1 1 5 β
β 4 6 1 2 1 4 β
β 5 1 3 β
β
(Four consecutive integers appear in each row; in the first, third and other odd numbered rows, the integers appear in the last four columns and increase from left to right; in the second, fourth and other even numbered rows, the integers appear in the first four columns and increase from right to left.)
In which column will the number 1,000 fall?
Answer Choices:
A. f i r s t f i r s t s e c o n d s e c o n d t h i r d t h i r d f o u r t h f o u r t h f i f t h f i f t h
Solution:
View Solution
Problem 10: What is the smallest integral value of k k 2 x ( k x β 4 ) β x 2 + 6 = 0 2 x ( k x β 4 ) β x 2 + 6 = 0
Answer Choices:
A. β 1 β 1 2 2 3 3 4 4 5 5
Solution:
View Solution
Problem 11: If ( a , b ) ( a , b ) ( c , d ) ( c , d ) y = m x + k y = m x + k ( a , b ) ( a , b ) ( c , d ) ( c , d ) a , c a , c m m
Answer Choices:
A. β£ a β c β£ 1 + m 2 β£ a β c β£ 1 + m 2 β β£ a + c β£ 1 + m 2 β£ a + c β£ 1 + m 2 β β£ a β c β£ 1 + m 2 1 + m 2 β β£ a β c β£ β β£ a β c β£ ( 1 + m 2 ) β£ a β c β£ ( 1 + m 2 ) β£ a β c β£ β£ m β£ β£ a β c β£ β£ m β£
Solution:
View Solution
Problem 12: If g ( x ) = 1 β x 2 g ( x ) = 1 β x 2 f ( g ( x ) ) = 1 β x 2 x 2 f ( g ( x ) ) = x 2 1 β x 2 β x β 0 x ξ = 0 f ( 1 / 2 ) f ( 1 / 2 )
Answer Choices:
A. 3 / 4 3 / 4 1 1 3 3 2 / 2 2 β / 2 2 2 β
Solution:
View Solution
Problem 13: Which of the following is equivalent to "If P P Q Q
Answer Choices:
A. P is true or Q is false.Q Q P P P P Q Q
Solution:
View Solution
Problem 14: Which statement is correct?
Answer Choices:
A. If x < 0 x < 0 x 2 > x x 2 > x x 2 > 0 x 2 > 0 x > 0 x > 0 x 2 > x x 2 > x x > 0 x > 0 x 2 > x x 2 > x x < 0 x < 0 x < 1 x < 1 x 2 < x x 2 < x
Solution:
View Solution
Problem 15: If x < β 2 x < β 2 β£ 1 β β£ 1 + x β£ β£ β£ 1 β β£ 1 + x β£ β£
Answer Choices:
A. 2 + x 2 + x β 2 β x β 2 β x x x β x β x β 2 β 2
Solution:
View Solution
Problem 16: A circle of radius r r R R R r r R β
Answer Choices:
A. 1 + 2 1 + 2 β 2 + 2 2 2 2 + 2 β β 2 β 1 2 2 2 β β 1 β 1 + 2 2 2 1 + 2 β β 2 ( 2 β 2 ) 2 ( 2 β 2 β )
Solution:
View Solution
Problem 17: If i 2 = β 1 i 2 = β 1 ( 1 + i ) 20 β ( 1 β i ) 20 ( 1 + i ) 2 0 β ( 1 β i ) 2 0
Answer Choices:
A. β 1024 β 1 0 2 4 β 1024 i β 1 0 2 4 i 0 0 1024 1 0 2 4 1024 i 1 0 2 4 i
Solution:
View Solution
Problem 18: If 8 3 = p log 8 β 3 = p 3 5 = q log 3 β 5 = q p p q , 10 5 q , log 1 0 β 5
Answer Choices:
A. p q p q 3 p + q 5 5 3 p + q β 1 + 3 p q p + q p + q 1 + 3 p q β 3 p q 1 + 3 p q 1 + 3 p q 3 p q β p 2 + q 2 p 2 + q 2
Solution:
View Solution
Problem 19: In the adjoining figure ABCD is a square and C M N C M N A B C D A B C D
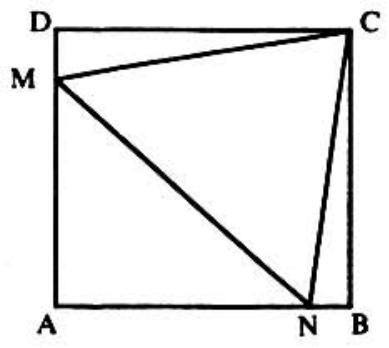
Answer Choices:
A. 2 3 β 3 2 3 β β 3 2 / 3 2 β / 3 1 β 3 / 3 1 β 3 β / 3 4 β 2 3 4 β 2 3 β 3 / 4 3 β / 4
Solution:
View Solution
Problem 20: Let T = 1 3 β 8 β 1 8 β 7 + 1 7 β 6 β 1 6 β 5 + 1 5 β 2 T = 3 β 8 β 1 β β 8 β β 7 β 1 β + 7 β β 6 β 1 β β 6 β β 5 β 1 β + 5 β β 2 1 β
Answer Choices:
A. T < 1 T < 1 T = 1 T = 1 1 < T < 2 1 < T < 2 T > 2 T > 2 T = 1 ( 3 β 8 ) ( 8 β 7 ) ( 7 β 6 ) ( 6 β 5 ) ( 5 β 2 ) T = ( 3 β 8 β ) ( 8 β β 7 β ) ( 7 β β 6 β ) ( 6 β β 5 β ) ( 5 β β 2 ) 1 β
Solution:
View Solution
Problem 21: In a geometric series of positive terms the difference between the fifth and fourth terms is 576, and the difference between the second and first terms is 9. What is the sum of the first five terms of this series?
Answer Choices:
A. 1061 1 0 6 1 1023 1 0 2 3 1024 1 0 2 4 768 7 6 8
Solution:
View Solution
Problem 22: The minimum value of sin β‘ A 2 β 3 cos β‘ A 2 sin 2 A β β 3 β cos 2 A β A A
Answer Choices:
A. β 18 0 β β 1 8 0 β 6 0 β 6 0 β 12 0 β 1 2 0 β 0 β 0 β
Solution:
View Solution
Problem 23: In the adjoining figure T P T P T β² Q T β² Q r r T T T β² T β² P T β² β² Q P T β² β² Q T β² β² T β² β² T P = 4 T P = 4 T β² Q = 9 T β² Q = 9 r r
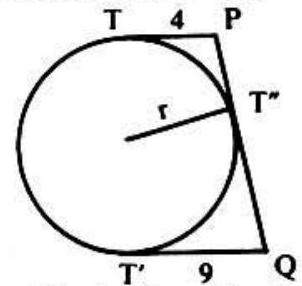
Answer Choices:
A. 25 / 6 2 5 / 6 6 6 25 / 4 2 5 / 4 25 / 6 , 6 , 25 / 4 2 5 / 6 , 6 , 2 5 / 4
Solution:
View Solution
Problem 24: A fair die is rolled six times. The probability of rolling at least a five at least five times is
Answer Choices:
A. 13 / 729 1 3 / 7 2 9 12 / 729 1 2 / 7 2 9 2 / 729 2 / 7 2 9 3 / 729 3 / 7 2 9
Solution:
View Solution
Problem 25: In parallelogram A B C D A B C D D P D P B C B C N N A B A B P P C C C Q C Q A D A D M M A B A B Q Q D P D P C Q C Q O O A B C D A B C D k k
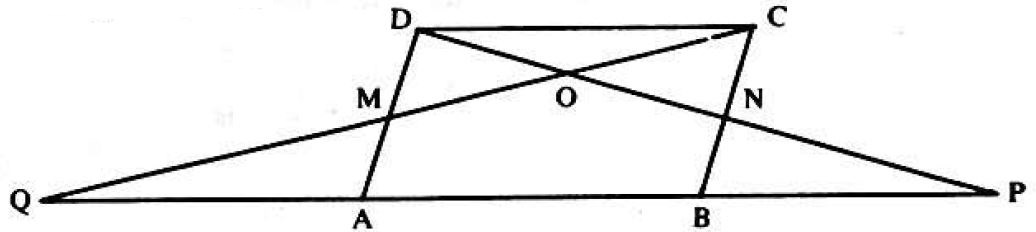
Answer Choices:
A. k k 6 k / 5 6 k / 5 9 k / 8 9 k / 8 5 k / 4 5 k / 4 2 k 2 k
Solution:
View Solution
Problem 26: The number of distinct positive integral divisors of ( 30 ) 4 ( 3 0 ) 4 ( 30 ) 4 ( 3 0 ) 4
Answer Choices:
A. 100 1 0 0 125 1 2 5 123 1 2 3 30 3 0
Solution:
View Solution
Problem 27: If f ( x ) = 3 x + 2 f ( x ) = 3 x + 2 x x β£ f ( x ) + 4 β£ < a β£ f ( x ) + 4 β£ < a β£ x + 2 β£ < b β£ x + 2 β£ < b a > 0 a > 0 b > 0 b > 0
Answer Choices:
A. b β©½ a / 3 b β©½ a / 3 b > a / 3 b > a / 3 a β©½ b / 3 a β©½ b / 3 a > b / 3 a > b / 3
Solution:
View Solution
Problem 28: Which of the following is satisfied by all numbers x x
x = a 1 3 + a 2 3 2 + β¦ + a 25 3 25 x = 3 a 1 β β + 3 2 a 2 β β + β¦ + 3 2 5 a 2 5 β β
where a 1 a 1 β 2 , a 2 2 , a 2 β 2 , β¦ , a 25 2 , β¦ , a 2 5 β 0 0 2 2
Answer Choices:
A. 0 β©½ x < 1 / 3 0 β©½ x < 1 / 3 1 / 3 β©½ x < 2 / 3 1 / 3 β©½ x < 2 / 3 2 / 3 β©½ x < 1 2 / 3 β©½ x < 1 0 β©½ x < 1 / 3 0 β©½ x < 1 / 3 2 / 3 β©½ x < 1 2 / 3 β©½ x < 1 1 / 2 β©½ x β©½ 3 / 4 1 / 2 β©½ x β©½ 3 / 4
Solution:
View Solution
Problem 29: For p = 1 , 2 , β¦ , 10 p = 1 , 2 , β¦ , 1 0 S p S p β p p 2 p β 1 2 p β 1 S 1 + S 2 + β¦ + S 10 S 1 β + S 2 β + β¦ + S 1 0 β
Answer Choices:
A. 80 , 000 8 0 , 0 0 0 80 , 200 8 0 , 2 0 0 80 , 400 8 0 , 4 0 0 80 , 600 8 0 , 6 0 0 80 , 800 8 0 , 8 0 0
Solution:
View Solution
Problem 30: A line segment is divided so that the lesser part is to the greater part as the greater part is to the whole. If R R
R [ R ( R 2 + 1 R ) + 1 R ] + 1 R R [ R ( R 2 + R 1 β ) + R 1 β ] + R 1 β
is
Answer Choices:
A. 2 2
B. 2 R 2 R
C. 1 / R 1 / R
D. 2 + 1 / R 2 + 1 / R
E. 2 + R 2 + R
Solution:
View Solution
The problems on this page are the property of the MAA's American Mathematics Competitions
