¶ 1975 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1975 AHSME problems, please refer below:
Problem 1: The value of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: For which real values of are the simultaneous equations
satisfied by at least one pair of real numbers ?
Answer Choices:
A. all
B. all
C. no values of
D. all
E. all
Solution:
Problem 3: Which of the following inequalities are satisfied for all real numbers , which satisfy the conditions , and
I.
II.
III.
Answer Choices:
A. None are satisfied.
B. II only
C. All are satisfied.
D. I only
E. III only
Solution:
Problem 4: If the side of one square is the diagonal of a second square, what is the ratio of the area of the first square to the area of the second?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: The polynomial is expanded in decreasing powers of . The second and third terms have equal value when evaluated at and , where and are positive numbers whose sum is one. What is the value of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: The sum of the first eighty positive odd integers subtracted from the sum of the first eighty positive even integers is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: For which non-zero real numbers is a positive integer?
Answer Choices:
A. for negative only
B. for positive only
C. only for an even integer
D. for all non-zero real numbers
E. for no non-zero real numbers
Solution:
Problem 8: If the statement "All shirts in this store are on sale." is false, then which of the following statements must be true?
I. All shirts in this store are not on sale.
II. There is some shirt in this store not on sale.
III. No shirt in this store is on sale.
IV. Not all shirts in this store are on sale.
Answer Choices:
A. II only
B. IV only
C. I and III only
D. II and IV only
E. I, II and IV only
Solution:
Problem 9: Let and be arithmetic progressions such that , and . Find the sum of the first one hundred terms of the progression
Answer Choices:
A.
B.
C.
D.
E. not enough information given to solve the problem
Solution:
Problem 10: The sum of the digits in base ten of , where is a positive integer, is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: Let be an interior point of circle other than the center of . From all chords of which pass through , and determine their midpoints. The locus of these midpoints is
Answer Choices:
A. a circle with one point deleted
B. a semicircle with one point deleted
C. a circle if the distance from to the center of is less than one half the radius of ; otherwise a circular arc of less than
D. a semicircle
E. a circle
Solution:
Problem 12: If and , which of the following conclusions is correct?
Answer Choices:
A.
B. or
C. or
D. or
E.
Solution:
Problem 13: The equation has
Answer Choices:
A. no real roots
B. exactly two distinct negative roots
C. exactly one negative root
D. no negative roots, but at least one positive root
E. none of these
Solution:
Problem 14: If the whatsis is so when the whosis is is and the so and so is is-so, what is the whosis-whatsis when the whosis is so, the so and so is so-so, and the is is two (whatsis, whosis, is and so are variables taking positive values)?
Answer Choices:
A. whosis-is-so
B. whosis
C. is
D. so
E. so and so
Solution:
Problem 15: In the sequence of numbers each term after the first two is equal to the term preceding it minus the term preceding that. The sum of the first one hundred terms of the sequence is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: If the first term of an infinite geometric series is a positive integer, the common ratio is the reciprocal of a positive integer, and the sum of the series is 3 , then the sum of the first two terms of the series is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: A man can commute either by train or by bus. If he goes to work on the train in the morning, he comes home on the bus in the afternoon; and if he comes home in the afternoon on the train, he took the bus in the morning. During days the man rode the train 9 times and rode the bus 8 times in the morning and 15 times in the afternoon. Find .
Answer Choices:
A.
B.
C.
D.
E. not enough information given to solve the problem
Solution:
Problem 18: A positive integer with three digits in its base ten representation is chosen at random, with each three-digit number having an equal chance of being chosen. The probability that is an integer is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: Which positive numbers satisfy the equation ?
Answer Choices:
A. 3 and 5 only
B. 3,5 and 15 only
C. only numbers of the form , where and are positive integers
D. all positive
E. none of these
Solution:
Problem 20: In the adjoining figure triangle is such that and . If is the midpoint of and , what is the length of ?
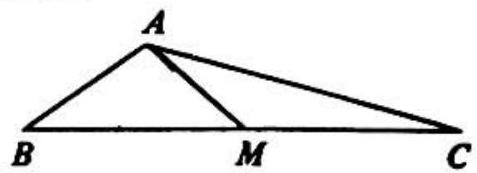
Answer Choices:
A.
B.
C.
D. not enough information
E. 9 given to solve the problem
Solution:
Problem 21: Suppose is defined for all real numbers for all ; and for all and . Which of the following statements are true?
I.
II. for all
III. for all
IV. if
Answer Choices:
A. III and IV only
B. I, II and IV only
C. All are true.
D. I, III and IV only
E. I, II and III only
Solution:
Problem 22: If and are prime integers and has distinct positive integral roots, then which of the following statements are true?
I. The difference of the roots is odd.
II. At least one root is prime.
III. is prime.
IV. is prime.
Answer Choices:
A. I only
B. II and III only
C. All are true.
D. II only
E. I, II and IV only
Solution:
Problem 23: In the adjoining figure and are adjacent sides of square is the midpoint of is the midpoint of ; and and intersect at . The ratio of the area of to the area of is
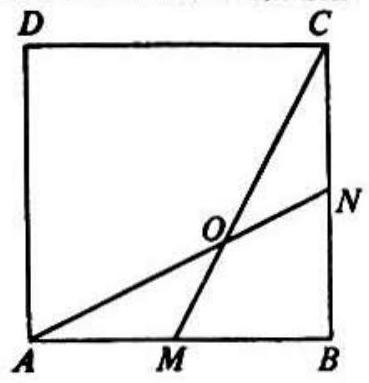
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: In triangle and , where . The circle with center and radius intersects at and intersects , extended if necessary, at and at may coincide with . Then
Answer Choices:
A. for no values of
B. only if
C. only if
D. only if
E. for all such that
Solution:
Problem 25: A woman, her brother, her son and her daughter (all relations by birth) are chess players. The worst player's twin (who is one of the four players) and the best player are of opposite sex. The worst player and the best player are the same age. Who is the worst player?
Answer Choices:
A. the woman
B. her brother
C. her son
D. her daughter
E. No solution is consistent with the given information.
Solution:
Problem 26: In acute triangle the bisector of meets side at . The circle with center and radius intersects side at ; and the circle with center and radius intersects side at . Then it is always true that
Answer Choices:
A.
B. is a trapezoid
C. is parallel to
D.
E.
Solution:
Problem 27: If and are distinct roots of , then equals
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 28: In triangle shown in the adjoining figure, is the midpoint of side , and . Points and are taken on and , respectively, and lines and intersect at . If then equals
.jpg)
Answer Choices:
A.
B.
C.
D.
E. not enough information given to solve the problem
Solution:
Problem 29: What is the smallest integer larger than ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 30: Let . Then equals
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions