¶ 1976 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1976 AHSME problems, please refer below:
Problem 1: If one minus the reciprocal of equals the reciprocal of , then equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: For how many real numbers is a real number?
Answer Choices:
A.
B.
C. infinitely many
D.
E. a finite number greater than two
Solution:
Problem 3: The sum of the distances from one vertex of a square with sides of length two to the midpoints of each of the sides of the square is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: Let a geometric progression with terms have first term one, common ratio and sum , where and are not zero. The sum of the geometric progression formed by replacing each term of the original progression by its reciprocal is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: How many integers greater than ten and less than one hundred, written in base ten notation, are increased by nine when their digits are reversed?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: If is a real number and the negative of one of the solutions of is a solution of , then the solutions of are
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: If is a real number, then the quantity is positive if and only if
Answer Choices:
A.
B.
C. or
D.
E.
Solution:
Problem 8: A point in the plane, both of whose rectangular coordinates are integers with absolute value less than or equal to four, is chosen at random, with all such points having an equal probability of being chosen. What is the probability that the distance from the point to the origin is at most two units?
Answer Choices:
A.
B.
C.
D.
E. the square of a rational number
Solution:
Problem 9: In triangle is the midpoint of is the midpoint of ; and is the midpoint of . If the area of is 96 , then the area of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: If and are real numbers and and , then the equation has a solution
Answer Choices:
A. for all choices of and
B. if and only if and
C. if and only if
D. if and only if
E. if and only if
Solution:
Problem 11: Which of the following statements is (are) equivalent to the statement "If the pink elephant on planet alpha has purple eyes, then the wild pig on planet beta does not have a long nose"?
I. "If the wild pig on planet beta has a long nose, then the pink elephant on planet alpha has purple eyes."
II. "If the pink elephant on planet alpha does not have purple eyes, then the wild pig on planet beta does not have a long nose."
III. "If the wild pig on planet beta has a long nose, then the pink elephant on planet alpha does not have purple eyes."
IV. "The pink elephant on planet alpha does not have purple eyes, or the wild pig on planet beta does not have a long nose."
Answer Choices:
A. I and III only
B. II and IV only
C. III only
D. III and IV only
E. II and III only
Solution:
Problem 12: A supermarket has 128 crates of apples. Each crate contains at least 120 apples and at most 144 apples. What is the largest integer such that there must be at least crates containing the same number of apples?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: If cows give cans of milk in days, how many days will it take cows to give cans of milk?
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 14: The measures of the interior angles of a convex polygon are in arithmetic progression. If the smallest angle is and the largest angle is , then the number of sides the polygon has is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: If is the remainder when each of the numbers 1059,1417 and 2312 is divided by , where is an integer greater than one, then equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: In triangles and . lengths and are all equal. Length is twice the length of the altitude of from to . Which of the following statements is (are) true?
I. and must be complementary.
II. and must be supplementary.
III. The area of must equal the area of .
IV. The area of must equal twice the area of .
Answer Choices:
A. II only
B. IV only
C. II and III only
D. III only
E. I and III only
Solution:
Problem 17: If 0 is an acute angle and , then equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: In the adjoining figure, is tangent at to the circle with center ; point is interior to the circle; and intersects the circle at . If and , then the radius of the circle is
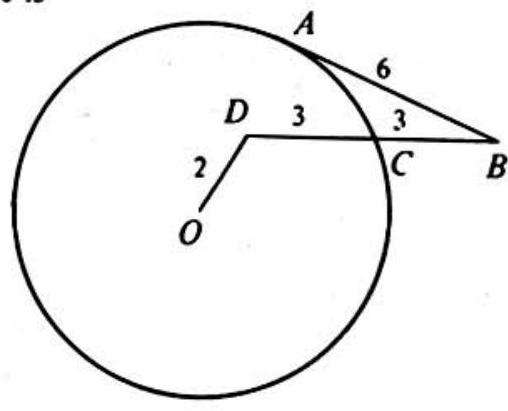
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: A polynomial has remainder three when divided by and remainder five when divided by . The remainder when is divided by is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: Let and be positive real numbers distinct from one. Then
Answer Choices:
A. For all values of and
B. If and only if
C. If and only if
D. If and only if
E. For none of these
Solution:
Problem 21: What is the smallest positive odd integer such that the product
is greater than 1000?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Given an equilateral triangle with side of length , consider the locus of all points in the plane of the triangle such that the sum of the squares of the distances from to the vertices of the triangle is a fixed number . This locus
Answer Choices:
A. is a circle if
B. Contains only three points if and is a circle if
C. Is a circle with positive radius only if
D. Contains only a finite number of points for any value of
E. Is none of these
Solution:
Problem 23: For integers and such that , let . Then is an integer
Answer Choices:
A. For all and
B. For all even values of and , but not for all and
C. For all odd values of and , but not for all and
D. If or , but not for all odd values of and
E. If is divisible by , but not for all even values of and
Solution:
Problem 24: In the adjoining figure, circle has diameter ; circle is tangent to circle and to at the center of circle ; and circle is tangent to circle , to circle and to . The ratio of the area of circle to the area of circle is
.jpg)
Answer Choices:
A.
B.
C.
D.
E. Not an integer
Solution:
Problem 25: For a sequence , define and, for all integers . If , then for all
Answer Choices:
A. If
B. If , but not if
C. If , but not if
D. If , but not if
E. For no value of
Solution:
Problem 26: In the adjoining figure, every point of circle is exterior to circle . Let and be the points of intersection of an internal common tangent with the two external common tangents. Then the length of is
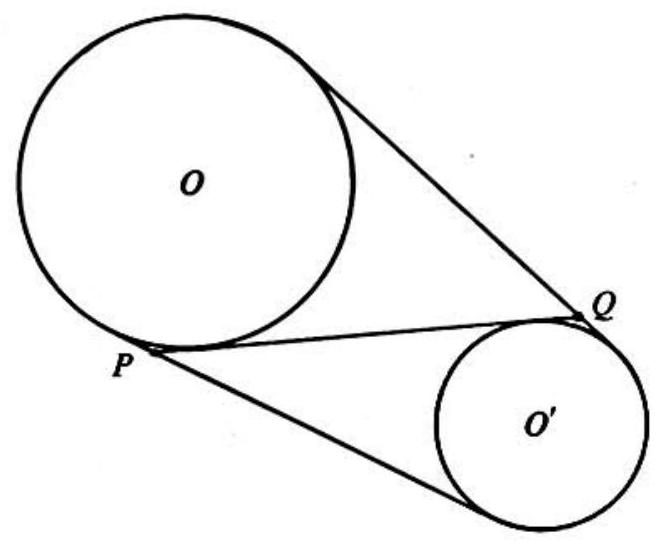
Answer Choices:
A. The average of the lengths of the internal and external common tangents
B. Equal to the length of an external common tangent if and only if circles and have equal radii
C. Always equal to the length of an external common tangent
D. Greater than the length of an external common tangent
E. The geometric mean of the lengths of the internal and external common tangents
Solution:
Problem 27: If
then equals
Answer Choices:
A.
B.
C.
D.
E. None of these
Solution:
Problem 28: Lines are distinct. All lines a positive integer, are parallel to each other. All lines a positive integer, pass through a given point . The maximum number of points of intersection of pairs of lines from the complete set is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 29: Ann and Barbara were comparing their ages and found that Barbara is as old as Ann was when Barbara was as old as Ann had been when Barbara was half as old as Ann is. If the sum of their present ages is 44 years, then Ann's age is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 30: How many distinct ordered triples satisfy the equations
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions