¶ 1977 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1977 AHSME problems, please refer below:
Problem 1: If and , then equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: Which one of the following statements is false? All equilateral triangles are
Answer Choices:
A.
B.
C. regular polygons
D. congruent to each other
E. similar to each other
Solution:
Problem 3: A man has in pennies, nickels, dimes, quarters and half dollars. If he has an equal number of coins of each kind then the total number of coins he has is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: In triangle and . If points and lie on sides , and , respectively, and and , then equals
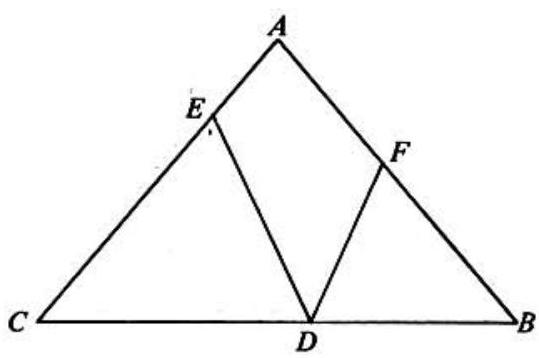
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 5: The set of all points such that the sum of the (undirected) distances from to two fixed points and equals the distance between and is
Answer Choices:
A. the line segment from to
B. the line passing through and
C. the perpendicular bisector of the line segment from to
D. an ellipse having positive area
E. a parabola
Solution:
Problem 6: If and are not zero, then equals
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 7: If , then equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: For every triple of non-zero real numbers, form the number
The set of all numbers formed is
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 9: In the adjoining figure and and all have equal length. Find the measure of .
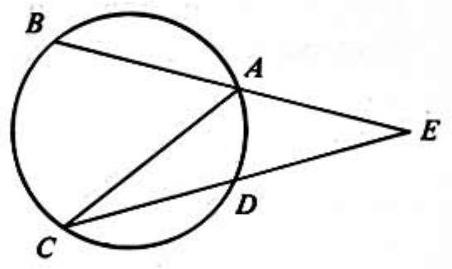
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: If , then equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: For each real number , let be the largest integer not exceeding (i.e., the integer such that ). Which of the following statements is (are) true?
I. for all
II. for all and
III. for all and
Answer Choices:
A.
B. I only
C. I and II only
D. III only
E.
Solution:
Problem 12: Al's age is 16 more than the sum of Bob's age and Carl's age, and the square of Al's age is 1632 more than the square of the sum of Bob's age and Carl's age. The sum of the ages of and Carl is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: If is a sequence of positive numbers such that for all positive integers , then the sequence is a geometric progression
Answer Choices:
A. for all positive values of and
B. if and only if
C. if and only if
D. if and only if
E. if and only if
Solution:
Problem 14: How many pairs ( ) of integers satisfy the equation ?
Answer Choices:
A.
B.
C.
D.
E. more than 4
Solution:
Problem 15: Each of the three circles in the adjoining figure is externally tangent to the other two, and each side of the triangle is tangent to two of the circles. If each circle has radius three, then the perimeter of the triangle is
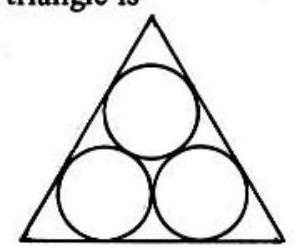
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: If , then the sum equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Three fair dice are tossed at random (i.e., all faces have the same probability of coming up). What is the probability that the three numbers turned up can be arranged to form an arithmetic progression with common difference one?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: If then
Answer Choices:
A.
B.
C.
D.
E. none of these answers
Solution:
Problem 19: Let be the point of intersection of the diagonals of convex quadrilateral , and let and be the centers of the circles circumscribing triangles and , respectively. Then
Answer Choices:
A. is a parallelogram
B. is a parallelogram if and only if is a rhombus
C. is a parallelogram if and only if is a rectangle
D. is a parallelogram if and only if is a parallelogram
E. none of the above are true
Solution:
Problem 20: For how many paths consisting of a sequence of horizontal and/or vertical line segments, with each segment connecting a pair of adjacent letters in the diagram below, is the word CONTEST spelled out as the path is traversed from beginning to end?
Answer Choices:
A.
B.
C.
D.
E. none of these answers
Solution:
Problem 21: For how many values of the coefficient do the equations
and
have a common real solution?
Answer Choices:
A.
B.
C.
D.
E. infinitely many
Solution:
Problem 22: If is a real valued function of the real variable , and is not identically zero, and for all and ,
then for all and
Answer Choices:
A.
B.
C.
D.
E. there is a positive number such that
Solution:
Problem 23: If the solutions of the equation are the cubes of the solutions of the equation , then
Answer Choices:
A.
B.
C.
D.
E. none of these answers
Solution:
Problem 24: Find the sum
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Determine the largest positive integer such that 1005 ! is divisible by .
Answer Choices:
A.
B.
C.
D.
E. none of these answers
Solution:
Problem 26: Let and be the lengths of sides and , respectively, of quadrilateral . If is the area of , then
Answer Choices:
A. if and only if is convex
B. if and only if is a rectangle
C. if and only if is a rectangle
D. if and only if is a parallelogram
E. if and only if is a parallelogram
Solution:
Problem 27: There are two spherical balls of different sizes lying in two corners of a rectangular room, each touching two walls and the floor. If there is a point on each ball which is 5 inches from each wall which that ball touches and 10 inches from the floor, then the sum of the diameters of the balls is
Answer Choices:
A. 20 inches
B. 30 inches
C. 40 inches
D. 60 inches
E. not determined by the given information
Solution:
Problem 28: Let . What is the remainder when the polynomial is divided by the polynomial ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 29: Find the smallest integer such that for all real numbers and .
Answer Choices:
A.
B.
C.
D.
E. There is no such integer
Solution:
Problem 30: If and are the lengths of a side, a shortest diagonal and a longest diagonal, respectively, of a regular nonagon, then
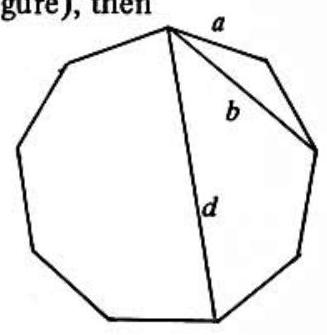
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions