¶ 1978 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1978 AHSME problems, please refer below:
Problem 1: If , then equals
Answer Choices:
A.
B.
C.
D. or
E. or
Solution:
Problem 2: If four times the reciprocal of the circumference of a circle equals the diameter of the circle, then the area of the circle is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: For all non-zero numbers and such that equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: If and , then
is equal to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Four boys bought a boat for . The first boy paid one half of the sum of the amounts paid by the other boys; the second boy paid one third of the sum of the amounts paid by the other boys; and the third boy paid one fourth of the sum of the amounts paid by the other boys. How much did the fourth boy pay?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: The number of distinct pairs of real numbers satisfying both of the following equations:
is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: Opposite sides of a regular hexagon are 12 inches apart. The length of each side, in inches, is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: If and the sequences and each are in arithmetic progression, then equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: If , then equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: If is a point on circle with center , then the set of all points in the plane of circle such that the distance between and is less than or equal to the distance between and any other point on circle is
Answer Choices:
A. the line segment from to
B. the ray beginning at and passing through
C. a ray beginning at
D. a circle whose center is
E. a circle whose center is
Solution:
Problem 11: If is positive and the line whose equation is is tangent to the circle whose equation is , then equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: In and points and lie on sides and , respectively. If lengths and are all equal, then the measure of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: If , and are non-zero numbers such that and are solutions of and and are solutions of , then equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: If an integer greater than 8 is a solution of the equation and the representation of in the base numeration system is 18, then the base representation of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: If and , then is
Answer Choices:
A.
B.
C.
D.
E. not completely determined by the given information
Solution:
Problem 16: In a room containing people, , at least one person has not shaken hands with everyone else in the room. What is the maximum number of people in the room that could have shaken hands with everyone else?
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 17: If is a positive number and is a function such that, for every positive number ,
then, for every positive number ,
is equal to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: What is the smallest positive integer such that ?
Answer Choices:
A.
B.
C.
D.
E. There is no such integer
Solution:
Problem 19: A positive integer not exceeding 100 is chosen in such a way that if , then the probability of choosing is , and if , then the probability of choosing is . The probability that a perfect square is chosen is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: If are non-zero real numbers such that
and
and , then equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: For all positive numbers distinct from 1,
equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: The following four statements, and only these, are found on a card:
On this card exactly one statement is false.
On this card exactly two statements are false.
On this card exactly three statements are false.
On this card exactly four statements are false.
(Assume each statement on the card is either true or false.) Among them the number of false statements is exactly
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: Vertex of equilateral triangle is in the interior of square , and is the point of intersection of diagonal and line segment . If length is then the area of is
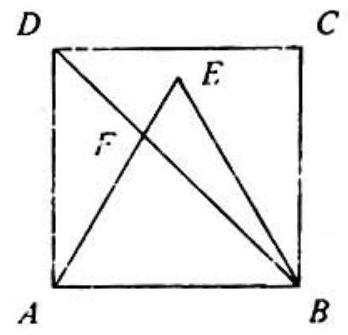
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: If the distinct non-zero numbers form a geometric progression with common ratio , then satisfies the equation
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: Let be a positive number. Consider the set of all points whose rectangular coordinates satisfy all of the following conditions:
(i)
(ii)
(iii)
(iv)
(v)
Answer Choices:
A. 3 sides
B. 4 sides
C. 5 sides
D. 6 sides
E. 7 sides
Solution:
Problem 26: In and . Circle is the circle with smallest radius which passes through and is tangent to . Let and be the points of intersection, distinct from , of circle with sides and , respectively. The length of segment is
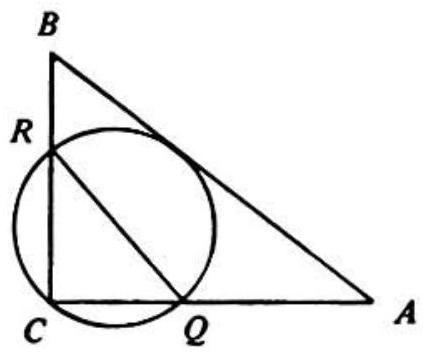
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 27: There is more than one integer greater than 1 which, when divided by any integer such that , has a remainder of 1. What is the difference between the two smallest such integers?
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 28: If is equilateral and is the midpoint of line segment for all positive integers , then the measure of equals
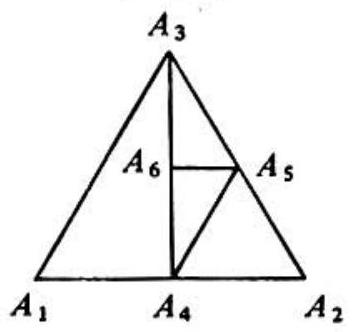
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 29: Sides and , respectively, of convex quadrilateral are extended past and to points and . Also, , , and ; and the area of is 10. The area of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 30: In a tennis tournament, women and men play, and each player plays exactly one match with every other player. If there are no ties and the ratio of the number of matches won by women to the number of matches won by men is , then equals
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions