¶ 1979 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1979 AHSME problems, please refer below:
Problem 1: If rectangle has area 72 square meters and and are the midpoints of sides and , respectively, then the area of rectangle in square meters is
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: For all non-zero real numbers and such that equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: In the adjoining figure, is a square, is an equilateral triangle and point is outside square . What is the measure of in degrees?
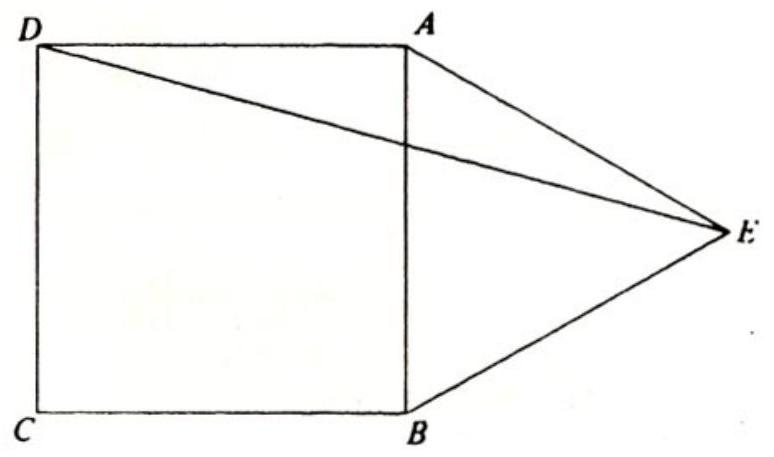
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: For all real numbers
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Find the sum of the digits of the largest even three digit number (in base ten representation) which is not changed when its unit's and hundred's digits are interchanged.
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6:
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: The square of an integer is called a perfect square. If is a perfect square, the next larger perfect square is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Find the area of the smallest region bounded by the graphs of and .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: The product of and equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: If is a tegular hexagon whose apothem (distance from the center to the midpoint of a side) is 2 , and is the midpoint of side for , then the area of quadrilateral is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: Find a positive integral solution to the equation
Answer Choices:
A.
B.
C.
D.
E. The equation has no positive integral solutions.
Solution:
Problem 12: In the adjoining figure, is the diameter of a semi-circle with center . Point lies on the extension of past ; point lies on the semi-circle, and is the point of intersection (distinct from ) of line segment : with the semi-circle. If length equals length , and the measure of is , then the measure of is
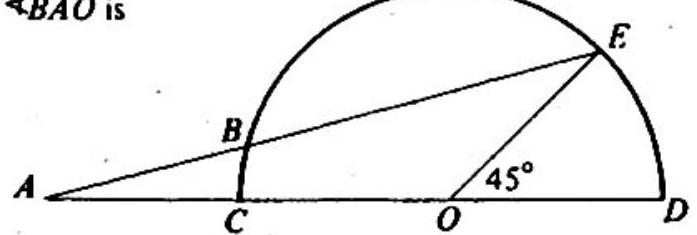
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: The inequality is satisfied if and only if
Answer Choices:
A. or (or both inequalities hold)
B. or (or both inequalities hold)
C.
D.
E. and
Solution:
Problem 14: In a certain sequence of numbers, the first number in the sequence is , and, for all , the product of the first numbers in the sequence is . The sum of the third and the fifth numbers in the sequence is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: Two identical jars are filled with alcohol solutions, the ratio of the volume of alcohol to the volume of water being in one jar and in the other jar. If the entire contents of the two jars are mixed together, the ratio of the volume of alcohol to the volume of water in the mixture is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: A circle with area is contained in the interior of a larger circle with area . If the radius of the larger circle is 3 , and if is an arithmetic progression, then the radius of the smaller circle is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Points and are distinct and lie, in the given order, on a straight line. Line segments and have lengths and , respectively. If line segments and may be rotated about points and , respectively, so that points and coincide, to form a triangle with positive area, then which of the following three inequalities must be satisfied?
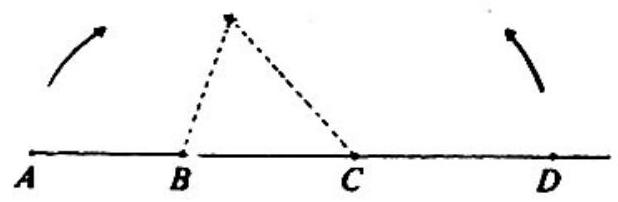
Answer Choices:
A. I only
B. II only
C. I and II only
D. II and III only
E. I, II and III
Solution:
Problem 18: To the nearest thousandth, is .301 and is .477 . Which of the following is the best approximation of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: Find the sum of the squares of all real numbers satisfying the equation
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: If and , then the radian measure of Arctan Arctan equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: The length of the hypotenuse of a right triangle is , and the radius of the inscribed circle is . The ratio of the area of the circle to the area of the triangle is
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 22: Find the number of pairs of integers which satisfy the equation
Answer Choices:
A.
B.
C.
D.
E. infinitely many
Solution:
Problem 23: The edges of a regular tetrahedron with vertices and each have length one. Find the least possible distance between a pair of points and . where is on edge and is on edge .
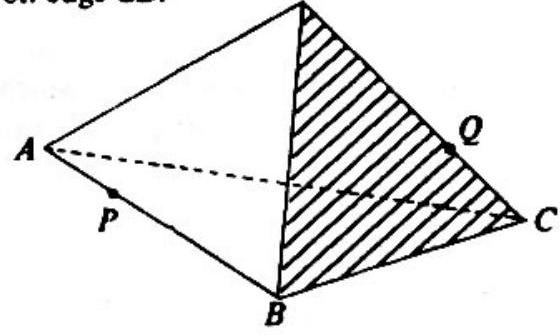
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: Sides and of (simple) quadrilateral have lengths 4,5 and 20, respectively. If vertex angles and are obtuse and , then side has length
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: If and are the quotient and remainder, respectively, when the polynomial is divided by , and if and are the quotient and remainder, respectively, when is divided by , then equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 26: The function satisfies the functional equation
for every pair of real numbers. If , then the number of integers for which is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 27: An ordered pair of integers, each of which has absolute value less than or equal to five, is chosen at random, with each such ordered pair having an equal likelihood of being chosen. What is the probability that the equation will not have distinct positive real roots?
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 28: Circles with centers and each have radius , where . The distance between each pair of centers is 2 . If is the point of intersection of circle and circle which is outside circle , and if is the point of intersection of circle and circle which is outside circle , then length equals
.jpg)
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 29: For each positive number , let
The minimum value of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 30: In is the midpoint of side and is on side . If the length of is and and , then the area of plus twice the area of equals
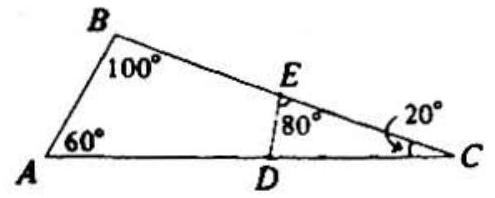
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions