¶ 1980 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1980 AHSME problems, please refer below:
Problem 1: The largest whole number such that seven times the number is less than is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: The degree of as a polynomial in is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: If the ratio of to is , what is the ratio of to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: In the adjoining figure, is an equilateral triangle and and are squares. The measure of is
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: If and are perpendicular diameters of circle , and , then the length of divided by the length of is
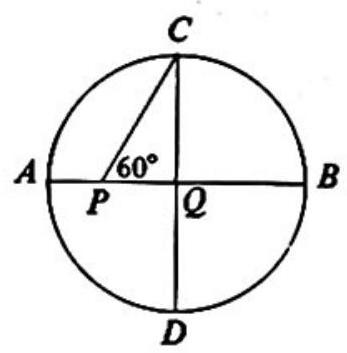
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: A positive number satisfies the inequality if and only if
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: Sides and of convex quadrilateral have lengths and , respectively; and is a right angle. The area of the quadrilateral is
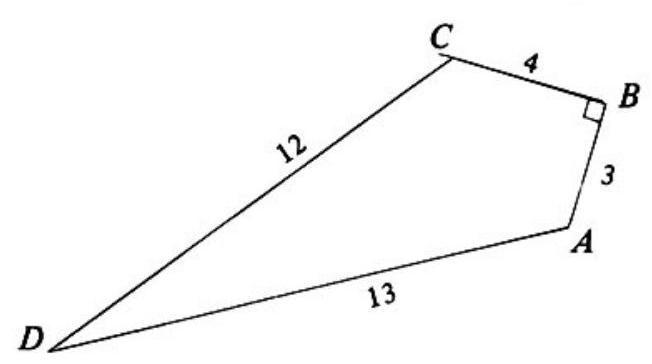
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: How many pairs of non-zero real numbers satisfy the equation
Answer Choices:
A. none
B.
C.
D. one pair for each
E. two pairs for each
Solution:
Problem 9: A man walks miles due west, turns to his left and walks miles in the new direction. If he finishes at a point miles from his starting point, then is
Answer Choices:
A.
B.
C.
D.
E. not uniquely determined by the given information
Solution:
Problem 10: The number of teeth in three meshed circular gears are , respectively. The angular speeds, in revolutions per minute, of are in the proportion
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: If the sum of the first terms and the sum of the first terms of a given arithmetic progression are and , respectively, then the sum of the first terms is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: The equations of and are and , respectively. Suppose makes twice as large an angle with the horizontal (measured counterclockwise from the positive -axis) as does , and that has times the slope of . If is not horizontal, then is
Answer Choices:
A.
B.
C.
D.
E. not uniquely determined by the given information
Solution:
Problem 13: A bug (of negligible size) starts at the origin on the co-ordinate plane. First it moves 1 unit right to . Then it makes a turn counterclockwise and travels a unit to . If it continues in this fashion, each time making a turn counterclockwise and traveling half as far as in the previous move, to which of the following points will it come closest?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: If the function defined by
satisfies for all real numbers except , then is
Answer Choices:
A.
B.
C.
D.
E. not uniquely determined by the given information
Solution:
Problem 15: A store prices an item in dollars and cents so that when sales tax is added no rounding is necessary because the result is exactly dollars where is a positive integer. The smallest value of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: Four of the eight vertices of a cube are vertices of a regular tetrahedron. Find the ratio of the surface area of the cube to the surface area of the tetrahedron.
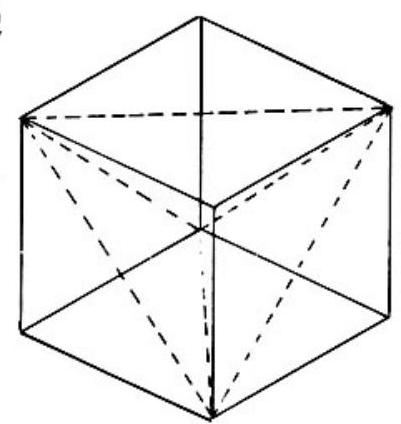
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: Given that , for how many integers is an integer?
Answer Choices:
A. none
B.
C.
D.
E.
Solution:
Problem 18: If and , then equals
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 19: Let and be three parallel chords of a circle on the same side of the center. The distance between and is the same as the distance between and . The lengths of the chords are , and . The radius of the circle is
Answer Choices:
A.
B.
C.
D.
E. not uniquely determined by the given information
Solution:
Problem 20: A box contains pennies, nickels and dimes. Six coins are drawn without replacement, with each coin having an equal probability of being chosen. What is the probability that the value of the coins drawn is at least cents?
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 21: In triangle , is the middpoint of side , and is a point on side such that and intersect at . The ratio of the area of to the area of quadrilateral is
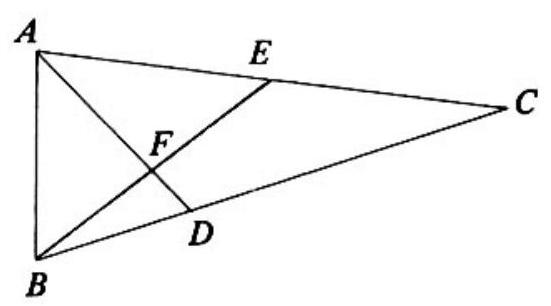
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 22: For each real number , let be the minimum of the numbers , , and . Then the maximum value of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: Line segments drawn from the vertex opposite the hypotenuse of a right triangle to the points trisecting the hypotenuse have lengths and , where is a real number such that . The length of the hypotenuse is
Answer Choices:
A.
B.
C.
D.
E. not uniquely determined by the given information
Solution:
Problem 24: For some real number , the polynomial is divisible by . Which of the following numbers is closest to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: In the non-decreasing sequence of odd integers each positive odd integer appears times. It is a fact that there are integers and such that, for all positive integers ,
where denotes the largest integer not exceeding . The sum equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 26: Four balls of radius are mutually tangent, three resting on the floor and the fourth resting on the others. A tetrahedron, each of whose edges has length , is circumscribed around the balls. Then equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 27: The sum equals
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 28: The polynomial is not divisible by if equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 29: How many ordered triples of integers satisfy the system of equations below?
Answer Choices:
A.
B.
C.
D. a finite number greater than two
E. infinitely many
Solution:
Problem 30: A six digit number (base ) is squarish if it satisfies the following conditions:
(i) none of its digits is zero;
(ii) it is a perfect square; and
(iii) the first of two digits, the middle two digits and the last two digits of the number are all perfect squares when considered as two digit numbers.
How many squarish numbers are there?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions