¶ 1981 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1981 AHSME problems, please refer below:
Problem 1: If then equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: Point is on side of square . If has length one and has length two, then the area of the square is
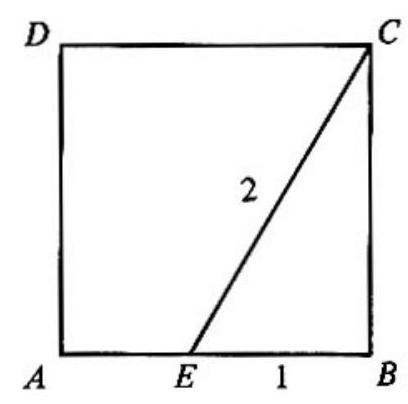
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: For equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: If three times the larger of two numbers is four times the smaller and the difference between the numbers is , then the larger of the two numbers is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: In trapezoid , sides and are parallel, and diagonal and side have equal length. If and , then
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: If , then equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: How many of the first one hundred positive integers are divisible by all of the numbers
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: For all positive numbers , the product equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: In the adjoining figure, is a diagonal of the cube. If has length , then the surface area of the cube is
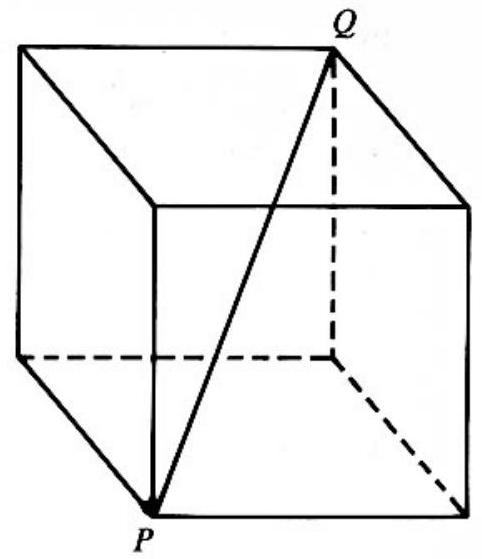
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: The lines and are symmetric to each other with respect to the line . If the equation of line is with and , then the equation of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: The three sides of a right triangle have integral lengths which form an arithmetic progression. One of the sides could have length
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: If and are positive numbers and , then the number obtained by increasing by and decreasing the result by exceeds if and only if
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 13: Suppose that at the end of any year, a unit of money has lost of the value it had at the beginning of that year. Find the smallest integer such that after years the unit of money will have lost at least of its value. (To the nearest thousandth is .)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: In a geometric sequence of real numbers, the sum of the first two terms is and the sum of the first six terms is . The sum of the first four terms is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: If and , then is
Answer Choices:
A.
B.
C.
D.
E. not uniquely determined
Solution:
Problem 16: The base three representation of is
The first digit (on the left) of the base nine representation of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: The function is not defined for , but, for all non-zero real numbers , . The equation is satisfied by
Answer Choices:
A. exactly real number
B. exactly real numbers
C. no real numbers
D. infinitely many, but not all, non-zero real numbers
E. all non-zero real numbers
Solution:
Problem 18: The number of real solutions to the equation
is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: In is the midpoint of side bisects and is the measure of . If sides and have lengths and , respectively, then length equals
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: A ray of light originates from point and travels in a plane, being reflected times between lines and , before striking a point (which may be on or ) perpendicularly and retracing its path to . If , what is the largest value can have?
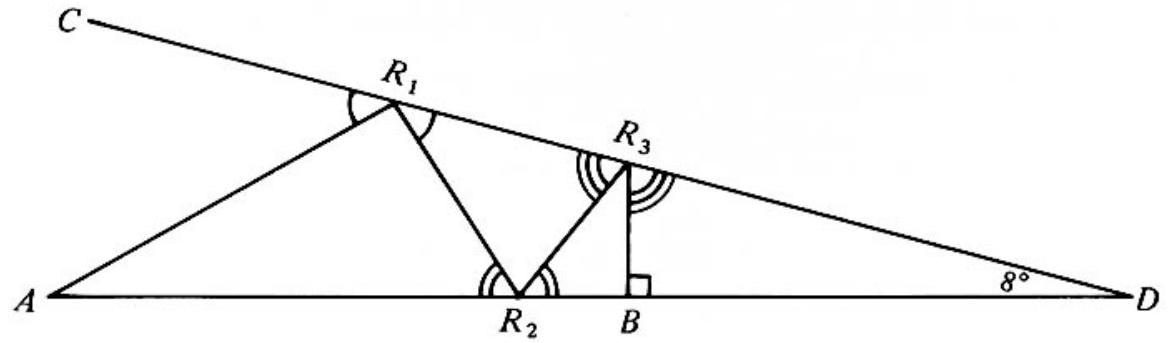
Answer Choices:
A.
B.
C.
D.
E. There is no largest value.
Solution:
Problem 21: In a triangle with sides of lengths and . The measure of the angle opposite the side of length is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: How many lines in a three-dimensional rectangular coordinate system pass through four distinct points of the form (), where and are positive integers not exceeding
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: Equilateral is inscribed in a circle. A second circle is tangent internally to the circumcircle at and tangent to sides and at points and . If side has length , then segment has length
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: If is a constant such that and , then for each positive integer equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: In triangle in the adjoining figure, and trisect \Varangle B A C. The lengths of and are and , respectively. The length of the shortest side of is
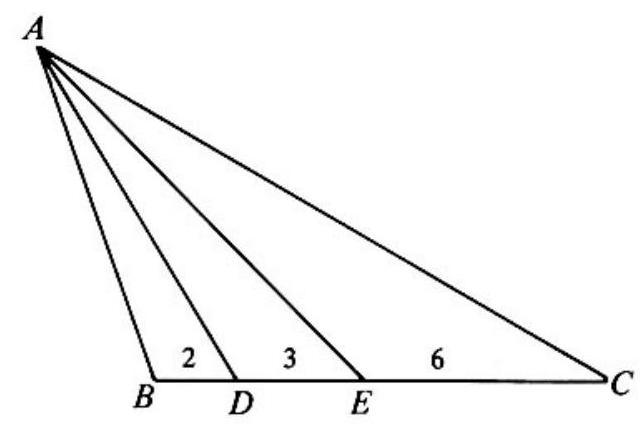
Answer Choices:
A.
B.
C.
D.
E. not uniquely determined by the given information
Solution:
Problem 26: Alice, Bob and Carol repeatedly take turns tossing a die. Alice begins; Bob always follows Alice; Carol always follows Bob; and Alice always follows Carol. Find the probability that Carol will be the first one to toss a six.
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 27: In the adjoining figure triangle is inscribed in a circle. Point lies on with , and point lies on with . Side and side each has length equal to the length of chord and . Chord intersects sides and at and , respectively. The ratio of the area of to the area of is
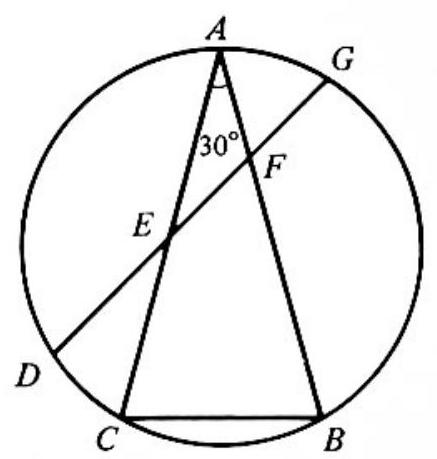
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 28: Consider the set of all equations , where are real constants and for . Let be the largest positive real number which satisfies at least one of these equations. Then
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 29: If , then the sum of the real solutions of
is equal to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 30: If are the solutions of the equation , then an equation whose solutions are is
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions