¶ 1982 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1982 AHSME problems, please refer below:
Problem 1: When the polynomial is divided by the polynomial , the remainder is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: If a number eight times as large as is increased by two, then one fourth of the result equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: Evaluate at .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: The perimeter of a semicircular region, measured in centimeters, is numerically equal to its area, measured in square centimeters. The radius of the semicircle, measured in centimeters, is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Two positive numbers and are in the ratio , where . If , then the smaller of and is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: The sum of all but one of the interior angles of a convex polygon equals . The remaining angle is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: If the operation is defined by , then which one of the following is false?
Answer Choices:
A. for all real and
B. for all real , and
C. for all real
D. for all real
E. for all real , and
Solution:
Problem 8: By definition and , where are positive integers and . If form an arithmetic progression with , then equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: A vertical line divides the triangle with vertices and in the -plane into two regions of equal area. The equation of the line is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: In the adjoining diagram, bisects bisects , and is parallel to . If , and , then the perimeter of is
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: How many integers with four different digits are there between and such that the absolute value of the difference between the first digit and the last digit is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: Let , where and are constants. If , then equals
Answer Choices:
A.
B.
C.
D.
E. not uniquely determined
Solution:
Problem 13: If and , then equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: In the adjoining figure, points and lie on line segment , and and are diameters of circles and , respectively. Circles and all have radius and the line is tangent to circle at . If intersects circle at points and , then chord has length
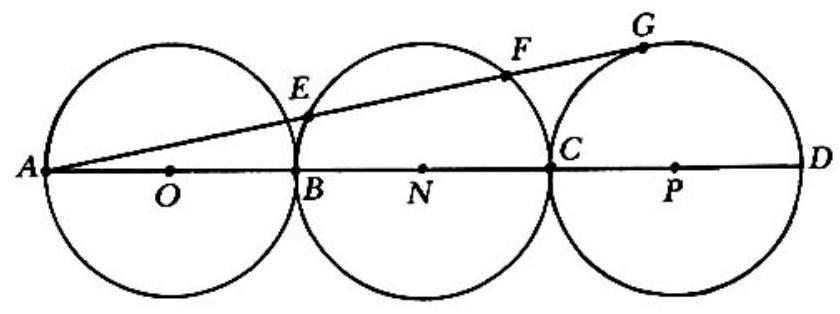
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 15: Let denote the greatest integer not exceedng . Let and satisfy the simultaneous equations
If is not an integer, then is
Answer Choices:
A. an integer
B. between and
C. between and
D. between and
E.
Solution:
Problem 16: In the adjoining figure, a wooden cube has edges of length meters. Square holes, of side meter, centered in each face are cut through to the opposite face. The edges of the holes are parallel to the edges of the cube. The entire surface area including the inside, in square meters, is
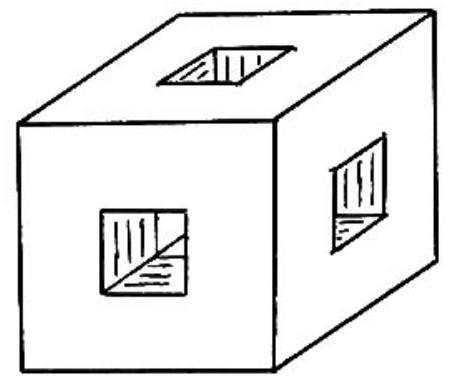
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: How many real numbers satisfy the equation
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: In the adjoining figure of a rectangular solid, and . Find the cosine of .
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 19: Let , for . The sum of the largest and smallest values of is
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 20: The number of pairs of positive integers which satisfy the equation is
Answer Choices:
A.
B.
C.
D. not finite
E. none of these
Solution:
Problem 21: In the adjoining figure, the triangle is a right triangle with . Median is perpendicular to median , and side . The length of is
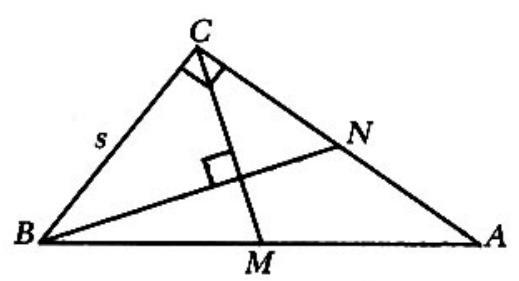
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: In a narrow alley of width a ladder of length is placed with its foot at a point between the walls. Resting against one wall at , a distance above the ground, the ladder makes a angle with the ground. Resting against the other wall at , a distance above the ground, the ladder makes a angle with the ground. The width is equal to
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 23: The lengths of the sides of a triangle are consecutive integers, and the largest angle is twice the smallest angle. The cosine of the smallest angle is
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 24: In the adjoining figure, the circle meets the sides of an equilateral triangle at six points. If and , then equals
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 25: The adjoining figure is a map of part of a city: the small rectangles are blocks and the spaces in between are streets. Each morning a student walks from intersection to intersection , always walking along streets shown, always going east or south. For variety, at each intersection where he has a choice, he chooses with probability (independent of all other choices) whether to go east or south. Find the probability that, on any given morning, he walks through intersection .
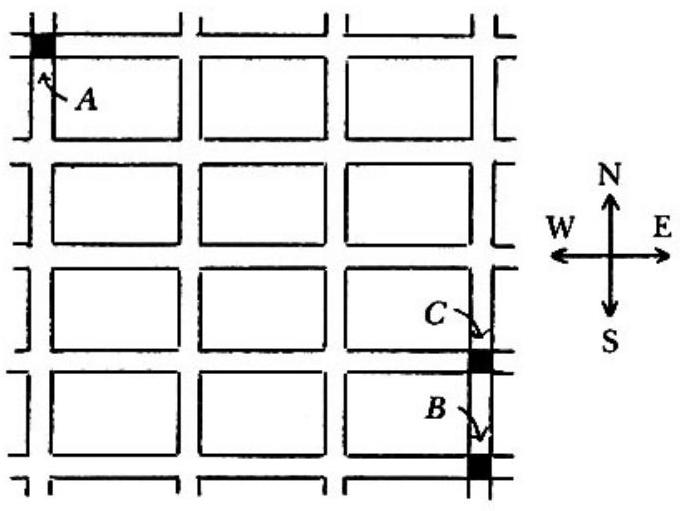
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 26: If the base representation of a perfect square is , where , then is
Answer Choices:
A.
B.
C.
D.
E. not uniquely determined
Solution:
Problem 27: Suppose is a solution of the polynomial equation
where , a and are real constants and . Which one of the following must also be a solution?
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 28: A set of consecutive positive integers beginning with is written on a blackboard. One number is erased. The average (arithmetic mean) of the remaining numbers is . What number was erased?
Answer Choices:
A.
B.
C.
D.
E. can not be determined
Solution:
Problem 29: Let and be three positive real numbers whose sum is . If no one of these numbers is more than twice any other, then the minimum possible value of the product is
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 30: Find the units digit in the decimal expansion of .
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions