¶ 1983 AHSME Problems and Solutions
Individual Problems and Solutions
For problems and detailed solutions to each of the 1983 AHSME problems, please refer below:
Problem 1: If and , then equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 2: Point is outside circle on the plane. At most how many points on are cm from
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 3: Three primes, and , satisfy and . Then equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 4: The area of the figure where sides and are parallel, as are sides and , and sides and , each side has length , and is
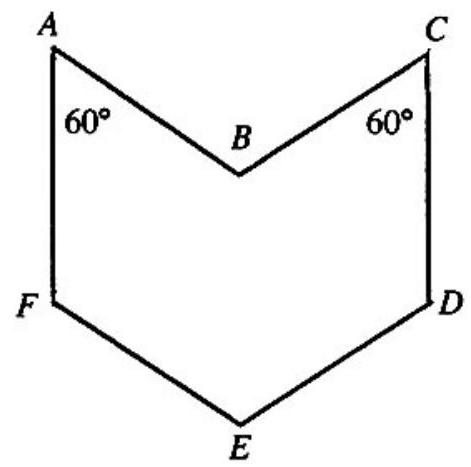
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 5: Triangle has a right angle at . If , then is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 6: When and are multiplied, the product is a polynomial of degree
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 7: Alice sells an item at less than the list price and receives of her selling price as her commission. Bob sells the same item at less than the list price and receives of his selling price as his commission. If they both get the same commission, then the list price is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 8: Let . Then for is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 9: In a certain population, the ratio of the number of women to the number of men is to . If the average (arithmetic mean) age of the women is and the average age of the men is , then the average age of the population is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 10: Segment is both a diameter of a circle of radius and a side of an equilateral triangle . The circle also intersects and at points and , respectively. The length of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 11: Simplify .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 12: If , then equals
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 13: If , and , and none of these quantities is , then equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 14: The units digit of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 15: Three balls marked and are placed in an urn. One ball is drawn, its number is recorded, and then the ball is returned to the urn. This process is repeated and then repeated once more, and each ball is equally likely to be drawn on each occasion. If the sum of the numbers recorded is , what is the probability that the ball numbered was drawn all three times?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 16: Let , where the digits are obtained by writing the integers through in order. The digit to the right of the decimal point is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 17: The diagram below shows several numbers in the complex plane. The circle is the unit circle centered at the origin. One of these numbers is the reciprocal of . Which one?
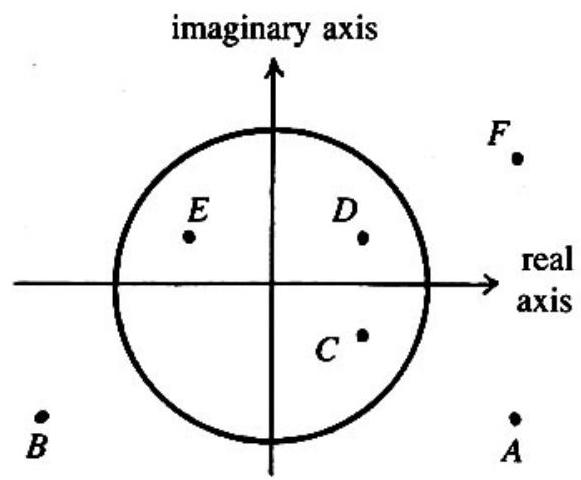
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 18: Let be a polynomial function such that, for all real ,
For all real is
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Problem 19: Point is on side of triangle . If and , then the length of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 20: If and are the roots of , and and are the roots of , then is necessarily
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 21: Find the smallest positive number from the numbers below.
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 22: Consider the two functions and , where the variable and the constants and are real numbers. Each such pair of constants and may be considered as a point in an -plane. Let be the set of such points for which the graphs of and do not intersect (in the -plane). The area of is
Answer Choices:
A.
B.
C.
D.
E. infinite
Solution:
Problem 23: In the adjoining figure the five circles are tangent to one another consecutively and to the lines and . If the radius of the largest circle is and that of the smallest one is , then the radius of the middle circle is
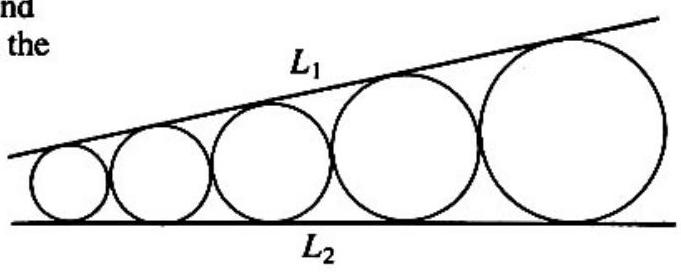
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 24: How many non-congruent right triangles are there such that the perimeter in cm and area in are numerically equal?
Answer Choices:
A. none
B.
C.
D.
E. infinitely many
Solution:
Problem 25: If and , then is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 26: The probability that event occurs is ; the probability that event occurs is . Let be the probability that both and occur. The smallest interval necessarily containing is the interval
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 27: A large sphere is on a horizontal field on a sunny day. At a certain time the shadow of the sphere reaches out a distance of m from the point where the sphere touches the ground. At the same instant a meter stick (held vertically with one end on the ground) casts a shadow of length m. What is the radius of the sphere in meters?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 28: Triangle in the figure has area . Points and , all distinct from , and , are on sides and respectively, and . If triangle and quadrilateral have equal areas, then that area is
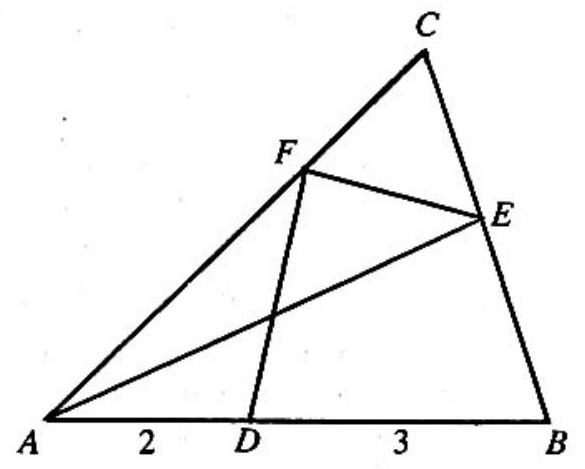
Answer Choices:
A.
B.
C.
D.
E. not uniquely determined
Solution:
Problem 29: A point lies in the same plane as a given square of side . Let the vertices of the square, taken counterclockwise, be and . Also, let the distances from to and , respectively, be and . What is the greatest distance that can be from if
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Problem 30: Distinct points and are on a semicircle with diameter and center . The point is on and . If , then equals
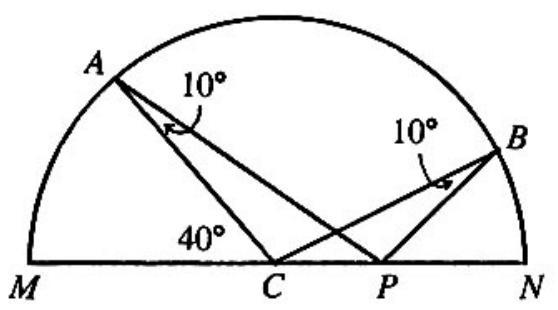
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions