¶ 1986 AIME Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 1986 AIME problems here.
Discussion Forum
Engage in discussion about the 1986 AIME math contest by visiting Random Math AIME 1986 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 1986 AIME problems, please refer below:
Problem 1: What is the sum of the solutions of the equation
Solution:
Problem 2: Evaluate the product
Solution:
Problem 3: If and , what is
Solution:
Problem 4: Determine if and satisfy the system of equations given below:
Solution:
Problem 5: What is the largest positive integer for which is divisible by
Solution:
Problem 6: The pages of a book are numbered through . When the page numbers of the book were added, one of the page numbers was mistakenly added twice, resulting in the incorrect sum of . What was the number of the page that was added twice?
Solution:
Problem 7: The increasing sequence consists of all those positive integers which are powers of or sums of distinct powers of . Find the term of this sequence (where is the term, is the term, and so on).
Solution:
Problem 8: Let be the sum of the base logarithms of all of the proper divisors of . (By a proper divisor of a natural number we mean a positive integral divisor other than and the number itself.) What is the integer nearest to
Solution:
Problem 9: In shown below, and . Moreover, is an interior point chosen so that the segments and are each of length , contain , and are parallel to the sides and , respectively. Find .
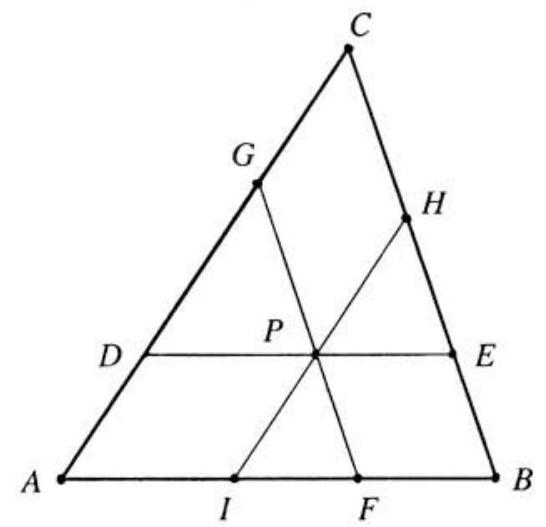
Solution:
Problem 10: In a parlor game the "magician" asks one of the participants to think of a three-digit number , where and represent digits in base in the order indicated. Then the magician asks this person to form the numbers and , to add these five numbers, and to reveal their sum, . If told the value of , the magician can identify the original number, . Play the role of the magician and determine if .
Solution:
Problem 11: The polynomial may be written in the form , where and the 's are constants. Find the value of .
Solution:
Problem 12: Let the sum of a set of numbers be the sum of its elements. Let be a set of positive integers, none greater than . Suppose no two disjoint subsets of have the same sum. What is the largest sum a set with these properties can have?
Solution:
Problem 13: In a sequence of coin tosses one can keep a record of the number of instances when a tail is immediately followed by a head, a head is immediately followed by a head, etc. We denote these by , etc. For example, in the sequence of coin tosses we observe that there are five , three , two and four subsequences. How many different sequences of coin tosses will contain exactly two , three , four and five subsequences?
Solution:
Problem 14: The shortest distances between an interior diagonal of a rectangular parallelpiped (box), , and the edges it does not meet are and . Determine the volume of .
Solution:
Problem 15: Let be a right triangle in the -plane with the right angle at . Given that the length of the hypotenuse is , and that the medians through and lie along the lines and , respectively, find the area of .
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions