¶ 1991 AIME Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 1991 AIME problems here.
Discussion Forum
Engage in discussion about the 1991 AIME math contest by visiting Random Math AIME 1991 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 1991 AIME problems, please refer below:
Problem 1: Find if and are positive integers such that
Solution:
Problem 2: Rectangle has sides of length and of length . Divide into congruent segments with points , and divide into 168 congruent segments with points . For , draw the segments . Repeat this construction on the sides and , and then draw the diagonal . Find the sum of the lengths of the parallel segments drawn.
Solution:
Problem 3: Expanding by the binomial theorem and doing no further manipulation gives
where for . For which is the largest?
Solution:
Problem 4: How many real numbers satisfy the equation
Solution:
Problem 5: Given a rational number, write it as a fraction in lowest terms and calculate the product of the resulting numerator and denominator. For how many rational numbers between and will be the resulting product?
Solution:
Problem 6: Suppose is a real number for which
Find . (For real is the greatest integer less than or equal to .)
Solution:
Problem 7: Find , where is the sum of the absolute values of all roots of the following equation:
Solution:
Problem 8: For how many real numbers does the quadratic equation have only integer roots for
Solution:
Problem 9: Suppose that and that , where is in lowest terms. Find .
Solution:
Problem 10: Two three-letter strings, and , are transmitted electronically. Each string is sent letter by letter. Due to faulty equipment, each of the six letters has a chance of being received incorrectly, as an when it should have been a , or as a when it should have been an . However, whether a given letter is received correctly or incorrectly is independent of the reception of any other letter. Let be the threeletter string received when is transmitted and let be the three-letter string received when is transmitted. Let be the probability that comes before in alphabetical order. When is written as a fraction in lowest terms, what is its numerator?
Solution:
Problem 11: Twelve congruent disks are placed on a circle of radius in such a way that the twelve disks cover , no two of the disks overlap, and so that each of the twelve disks is tangent to its two neighbors. The resulting arrangement of disks is shown in the figure to the right. The sum of the areas of the twelve disks can be written in the form , where are positive integers and is not divisible by the square of any prime. Find .
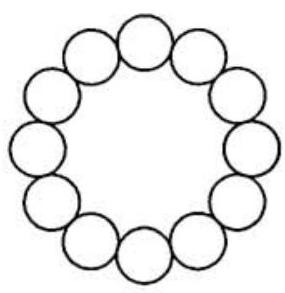
Solution:
Problem 12: Rhombus is inscribed in rectangle so that vertices , and are interior points on sides , and , respectively. It is given that , and . Let , in lowest terms, denote the perimeter of . Find .
Solution:
Problem 13: A drawer contains a mixture of red socks and blue socks, at most in all. It so happens that, when two socks are selected randomly without replacement, there is a probability of exactly that both are red or both are blue. What is the largest possible number of red socks in the drawer that is consistent with this data?
Solution:
Problem 14: A hexagon is inscribed in a circle. Five of the sides have length and the sixth, denoted by , has length . Find the sum of the lengths of the three diagonals that can be drawn from .
Solution:
Problem 15: For positive integer , define to be the minimum value of the sum
where are positive real numbers whose sum is . There is a unique positive integer for which is also an integer. Find this .
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions