¶ 1992 AIME Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 1992 AIME problems here.
Discussion Forum
Engage in discussion about the 1992 AIME math contest by visiting Random Math AIME 1992 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 1992 AIME problems, please refer below:
Problem 1: Find the sum of all positive rational numbers that are less than and that have denominator when written in lowest terms.
Solution:
Problem 2: A positive integer is called "ascending" if, in its decimal representation, there are at least two digits and each digit is less than any digit to its right. How many ascending positive integers are there?
Solution:
Problem 3: A tennis player computes her "win ratio" by dividing the number of matches she has won by the total number of matches she has played. At the start of a weekend, her win ratio is exactly . During the weekend she plays four matches, winning three and losing one. At the end of the weekend her win ratio is greater than . What is the largest number of matches that she could have won before the weekend began?
Solution:
Problem 4: In Pascal's triangle, each entry is the sum of the two entries above it. The first few rows of the triangle are shown below.
In which row of Pascal's triangle do three consecutive entries occur that are in the ratio
Solution:
Problem 5: Let be the set of all rational numbers , that have a repeating decimal expansion of the form
where the digits are not necessarily distinct. To write the elements of as fractions in lowest terms, how many different numerators are required?
Solution:
Problem 6: For how many pairs of consecutive integers in is no carrying required when the two integers are added?
Solution:
Problem 7: Faces and of tetrahedron meet at an angle of . The area of face is , the area of face is , and . Find the volume of the tetrahedron.
Solution:
Problem 8: For any sequence of real numbers , define to be the sequence , whose term is . Suppose that all of the terms of the sequence are , and that . Find .
Solution:
Problem 9: Trapezoid has sides , and , with parallel to . A circle with center on is drawn tangent to and . Given that , where and are relatively prime positive integers, find .
Solution:
Problem 10: Consider the region in the complex plane that consists of all points such that both and have real and imaginary parts between and inclusive. What is the integer that is nearest the area of (If with and real, then is the conjugate of .)
Solution:
Problem 11: Lines and both pass through the origin and make first-quadrant angles of and radians, respectively, with the positive -axis. For any line , the transformation produces another line as follows: is reflected in , and the resulting line is then reflected in . Let , and for integer define . Given that is the line , find the smallest positive integer for which .
Solution:
Problem 12: In a game of Chomp, two players alternately take "bites" from a -by- grid of unit squares. To take a bite, the player chooses one of the remaining squares, then removes ("eats") all squares found in the quadrant defined by the left edge (extended upward) and the lower edge (extended rightward) of the chosen square. For example, the bite determined by the shaded square in the diagram would remove the shaded square and the four squares marked by . (The squares with two or more dotted edges have been removed from the original board in previous moves.) The object of the game is to make one's opponent take the last bite. The diagram shows one of the many subsets of the set of unit squares that can occur during games of Chomp. How many different subsets are there in all? Include the full board and the empty board in your count.
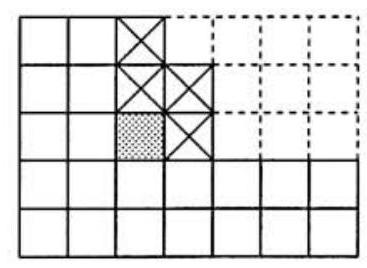
Solution:
Problem 13: Triangle has and . What is the largest area that this triangle can have?
Solution:
Problem 14: In triangle , and are on sides , and , respectively. Given that , and are concurrent at the point , and that
find the value of
Solution:
Problem 15: Define a positive integer to be a "factorial tail" if there is some positive integer such that the base-ten representation of ends with exactly zeros. How many positive integers less than are not factorial tails?
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions