¶ 1998 AIME Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 1998 AIME problems is available here.
Discussion Forum
Engage in discussion about the 1998 AIME math contest by visiting Random Math AIME 1998 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 1998 AIME problems, please refer below:
Problem 1: For how many values of is the least common multiple of the positive integers , and
Solution:
Problem 2: Find the number of ordered pairs of positive integers that satisfy and .
Solution:
Problem 3: The graph of partitions the plane into several regions. What is the area of the bounded region?
Solution:
Problem 4: Nine tiles are numbered , respectively. Each of three players randomly selects and keeps three of the tiles, and sums those three values. The probability that all three players obtain an odd sum is , where and are relatively prime positive integers. Find .
Solution:
Problem 5: Given that , find .
Solution:
Problem 6: Let be a parallelogram. Extend though to a point , and let meet at and at . Given that and , find .
Solution:
Problem 7: Let be the number of ordered quadruples of positive odd integers that satisfy . Find .
Solution:
Problem 8: Except for the first two terms, each term of the sequence is obtained by subtracting the preceding term from the one before that. The last term of the sequence is the first negative term encountered. What positive integer produces a sequence of maximum length?
Solution:
Problem 9: Two mathematicians take a morning coffee break each day. They arrive at the cafeteria independently, at random times between a.m. and a.m., and stay for exactly minutes. The probability that either one arrives while the other is in the cafeteria is , and , where , and are positive integers, and is not divisible by the square of any prime. Find .
Solution:
Problem 10: Eight spheres of radius 100 are placed on a flat surface so that each sphere is tangent to two others and their centers are the vertices of a regular octagon. A ninth sphere is placed on the flat surface so that it is tangent to each of the other eight spheres. The radius of this last sphere is , where , and are positive integers, and is not divisible by the square of any prime. Find .
Solution:
Problem 11: Three of the edges of a cube are , and , and is an interior diagonal. Points , and are on , and , respectively, so that , , and . What is the area of the polygon that is the intersection of plane and the cube?
Solution:
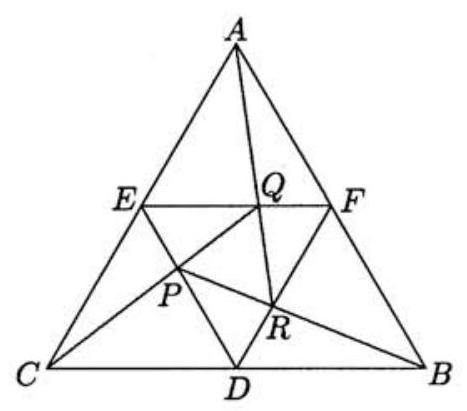
Problem 12: Let be equilateral, and , and be the midpoints of , and , respectively. There exist points , and on , , and , respectively, with the property that is on is on , and is on . The ratio of the area of triangle to the area of triangle is , where , and are integers, and is not divisible by the square of any prime. What is
Solution:
Problem 13: If is a set of real numbers, indexed so that , its complex power sum is defined to be , where . Let be the sum of the complex power sums of all nonempty subsets of . Given that and , where and are integers, find .
Solution:
Problem 14: An rectangular box has half the volume of an rectangular box, where , and are integers, and . What is the largest possible value of
Solution:
Problem 15: Define a domino to be an ordered pair of distinct positive integers. A proper sequence of dominos is a list of distinct dominos in which the first coordinate of each pair after the first equals the second coordinate of the immediately preceding pair, and in which and do not both appear for any and . Let be the set of all dominos whose coordinates are no larger than 40 . Find the length of the longest proper sequence of dominos that can be formed using the dominos of .
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions