¶ 1999 AIME Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 1999 AIME problems here.
Discussion Forum
Engage in discussion about the 1999 AIME math contest by visiting Random Math AIME 1999 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 1999 AIME problems, please refer below:
Problem 1: Find the smallest prime that is the fifth term of an increasing arithmetic sequence, all four preceding terms also being prime.
Solution:
Problem 2: Consider the parallelogram with vertices , and . A line through the origin cuts this figure into two congruent polygons. The slope of the line is , where and are relatively prime positive integers. Find .
Solution:
Problem 3: Find the sum of all positive integers for which is a perfect square.
Solution:
Problem 4: The two squares shown share the same center and have sides of length . The length of is and the area of octagon is , where and are relatively prime positive integers. Find .
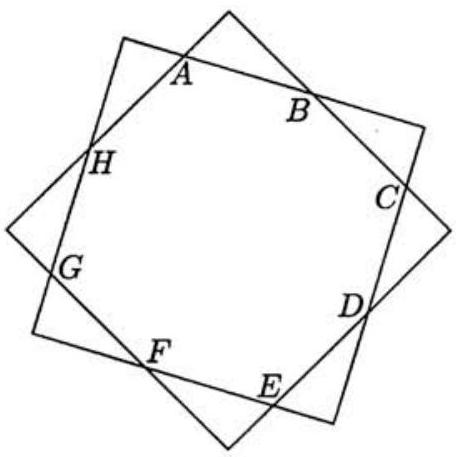
Solution:
Problem 5: For any positive integer , let be the sum of the digits of , and let be . For example, . How many values do not exceed
Solution:
Problem 6: A transformation of the first quadrant of the coordinate plane maps each point to the point . The vertices of quadrilateral are , , and . Let be the area of the region enclosed by the image of quadrilateral . Find the greatest integer that does not exceed .
Solution:
Problem 7: There is a set of switches, each of which has four positions, called , and . When the position of any switch changes, it is only from to , from to , from to , or from to . Initially each switch is in position . The switches are labeled with the different integers , where , and take on the values . At step of a -step process, the th switch is advanced one step, and so are all the other switches whose labels divide the label on the th switch. After step has been completed, how many switches will be in position
Solution:
Problem 8: Let be the set of ordered triples of nonnegative real numbers that lie in the plane . Let us say that supports when exactly two of the following are true: . Let consist of those triples in that support . The area of divided by the area of is , where and are relatively prime positive integers. Find .
Solution:
Problem 9: A function is defined on the complex numbers by , where and are positive numbers. This function has the property that the image of each point in the complex plane is equidistant from that point and the origin. Given that and that , where and are relatively prime positive integers, find .
Solution:
Problem 10: Ten points in the plane are given, with no three collinear. Four distinct segments joining pairs of these points are chosen at random, all such segments being equally likely. The probability that some three of the segments form a triangle whose vertices are among the ten given points is , where and are relatively prime positive integers. Find .
Solution:
Problem 11: Given that , where angles are measured in degrees, and and are relatively prime positive integers that satisfy , find .
Solution:
Problem 12: The inscribed circle of triangle is tangent to at , and its radius is . Given that and , find the perimeter of the triangle.
Solution:
Problem 13: Forty teams play a tournament in which every team plays every other team exactly once. No ties occur, and each team has a chance of winning any game it plays.The probability that no two teams win the same number of games is , where and are relatively prime positive integers. Find .
Solution:
Problem 14: Point is located inside triangle so that angles , and are all congruent. The sides of the triangle have lengths , and , and the tangent of angle is , where and are relatively prime positive integers. Find .
Solution:
Problem 15: Consider the paper triangle whose vertices are , and .The vertices of its midpoint triangle are the midpoints of its sides. A triangular pyramid is formed by folding the triangle along the sides of its midpoint triangle.What is the volume of this pyramid?
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions