¶ 2007 AIME II Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2007 AIME II problems here.
Discussion Forum
Engage in discussion about the 2007 AIME II math contest by visiting Random Math AIME II 2007 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2007 AIME II problems, please refer below:
Problem 1: A mathematical organization is producing a set of commemorative license plates. Each plate contains a sequence of five characters chosen from the four letters in and the four digits in . No character may appear in a sequence more times than it appears among the four letters in or the four digits in . A set of plates in which each possible sequence appears exactly once contains license plates. Find .
Solution:
Problem 2: Find the number of ordered triples where , and are positive integers, is a factor of is a factor of , and .
Solution:
Problem 3: Square has side length , and points and are exterior to the square such that and . Find .

Solution:
Problem 4: The workers in a factory produce widgets and whoosits. For each product, production time is constant and identical for all workers, but not necessarily equal for the two products. In one hour, workers can produce widgets and whoosits. In two hours, workers can produce widgets and whoosits. In three hours, workers can produce widgets and whoosits. Find .
Solution:
Problem 5: The graph of the equation is drawn on graph paper with each square representing one unit in each direction. How many of the by graph paper squares have interiors lying entirely below the graph and entirely in the first quadrant?
Solution:
Problem 6: An integer is called parity-monotonic if its decimal representation satisfies if is odd, and if is even. How many four-digit parity-monotonic integers are there?
Solution:
Problem 7: Given a real number , let denote the greatest integer less than or equal to . For a certain integer , there are exactly positive integers such that and divides for all such that . Find the maximum value of for .
Solution:
Problem 8: A rectangular piece of paper measures units by units. Several lines are drawn parallel to the edges of the paper. A rectangle determined by the intersections of some of these lines is called basic if
(i) all four sides of the rectangle are segments of drawn line segments, and
(ii) no segments of drawn lines lie inside the rectangle.
Given that the total length of all lines drawn is exactly units, let be the maximum possible number of basic rectangles determined. Find the remainder when is divided by .
Solution:
Problem 9: Rectangle is given with and . Points and lie on and respectively, such that . The inscribed circle of triangle is tangent to at point , and the inscribed circle of triangle is tangent to at point . Find .
Solution:
Problem 10: Let be a set with six elements. Let be the set of all subsets of . Subsets and of , not necessarily distinct, are chosen independently and at random from . The probability that is contained in at least one of or is , where , and are positive integers, is prime, and and are relatively prime. Find . (The set is the set of all elements of which are in .)
Solution:
Problem 11: Two long cylindrical tubes of the same length but different diameters lie parallel to each other on a flat surface. The larger tube has radius and rolls along the surface toward the smaller tube, which has radius . It rolls over the smaller tube and continues rolling along the flat surface until it comes to rest on the same point of its circumference as it started, having made one complete revolution. If the smaller tube never moves, and the rolling occurs with no slipping, the larger tube ends up a distance from where it starts. The distance can be expressed in the form , where , and are integers and is not divisible by the square of any prime. Find .
Solution:
Problem 12: The increasing geometric sequence consists entirely of integral powers of . Given that
find .
Solution:
Problem 13: A triangular array of squares has one square in the first row, two in the second, and, in general, squares in the th row for . With the exception of the bottom row, each square rests on two squares in the row immediately below, as illustrated in the figure. In each square of the eleventh row, a or a is placed. Numbers are then placed into the other squares, with the entry for each square being the sum of the entries in the two squares below it. For how many initial distributions of 's and 's in the bottom row is the number in the top square a multiple of
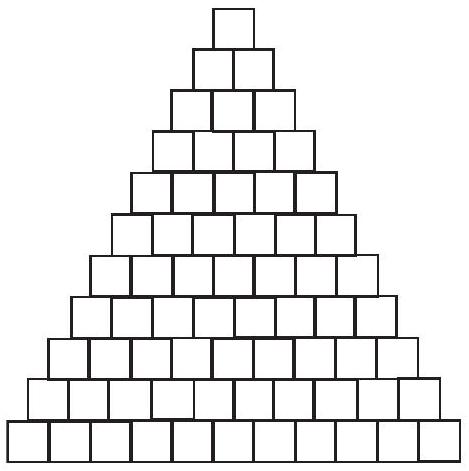
Solution:
Problem 14: Let be a polynomial with real coefficients such that , and for all . Find .
Solution:
Problem 15: Four circles , and with the same radius are drawn in the interior of triangle such that is tangent to sides and to and to and , and is externally tangentto , and . If the sides of triangle are , and , the radius of can be represented in the form , where and are relatively prime positive integers. Find .
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions