¶ 2017 AIME I Problems and Solutions
Problem Set Workbook
Access the downloadable workbook for 2017 AIME I problems here.
Discussion Forum
Engage in discussion about the 2017 AIME I math contest by visiting Random Math AIME I 2017 Forum
Individual Problems and Solutions
For problems and detailed solutions to each of the 2017 AIME I problems, please refer below:
Problem 1: Fifteen distinct points are designated on : the vertices , and ; other points on side other points on side ; and other points on side . Find the number of triangles with positive area whose vertices are among these points.
Solution:
Problem 2: When each of , and is divided by the positive integer , the remainder is always the positive integer . When each of , and is divided by the positive integer , the remainder is always the positive integer . Find .
Solution:
Problem 3: For a positive integer , let be the units digit of . Find the remainder when
is divided by .
Solution:
Problem 4: A pyramid has a triangular base with side lengths , and . The three edges of the pyramid from the three corners of the base to the fourth vertex of the pyramid all have length . The volume of the pyramid is , where and are positive integers, and is not divisible by the square of any prime. Find .
Solution:
Problem 5: A rational number written in base eight is , where all digits are nonzero. The same number in base twelve is . Find the base-ten number .
Solution:
Problem 6: A circle is circumscribed around an isosceles triangle whose two congruent angles have degree measure . Two points are chosen independently and uniformly at random on the circle, and a chord is drawn between them. The probability that the chord intersects the triangle is . Find the difference between the largest and smallest possible values of .
Solution:
Problem 7: For nonnegative integers and with , let . Let denote the sum of all , where and are nonnegative integers with . Find the remainder when is divided by .
Solution:
Problem 8: Two real numbers and are chosen independently and uniformly at random from the interval . Let and be two points in the plane with . Let and be points on the same side of line such that the degree measures of and are and , respectively, and and are both right angles. The probability that is equal to , where and are relatively prime positive integers. Find .
Solution:
Problem 9: Let , and for each integer let . Find the least such that is a multiple of .
Solution:
Problem 10: Let , and , where . Let be the unique complex number with the properties that is a real number and the imaginary part of is the greatest possible. Find the real part of .
Solution:
Problem 11: Consider arrangements of the numbers in a array. For each such arrangement, let , and be the medians of the numbers in rows and respectively, and then let be the median of . Let be the number of arrangements for which . Find the remainder when is divided by .
Solution:
Problem 12: Call a set product-free if there do not exist (not necessarily distinct) such that . For example, the empty set and the set are product-free, whereas the sets and are not product-free. Find the number of product-free subsets of the set .
Solution:
Problem 13: For every , let be the least positive integer with the following property: For every , there is always a perfect cube in the range . Find the remainder when
is divided by .
Solution:
Problem 14: Let and satisfy and . Find the remainder when is divided by .
Solution:
Problem 15: The area of the smallest equilateral triangle with one vertex on each of the sides of the right triangle with side lengths , and , as shown, is , where , , and are positive integers, and are relatively prime, and is not divisible by the square of any prime. Find .
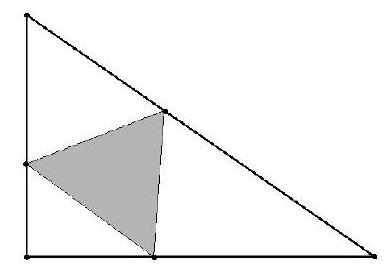
Solution:
The problems on this page are the property of the MAA's American Mathematics Competitions